Physics 101 Exam 2
8 November 2002 Prof L. Weinstein

There are 16 problems. Please give a short explanation for all multiple choice questions. Show your work for all numerical answers.

G = $6.67\cdot10^{-11}$ N$\cdot$m$^2$/kg$^2$

Earth's mass $M_e = 6\cdot 10^{24}$ kg

Earth's radius $R_e = 6.4\cdot 10^6$ m

Moon's mass $M_m = 7\cdot 10^{22}$ kg

Moon's radius $R_m = 1.7\cdot 10^6$ m

Earth-Moon distance $d_{E-m} = 3.8\cdot 10^8$ m

Earth-Sun distance $d_{E-S} = 1.5\cdot10^{11}$ m
 
 

1. Which has more potential energy, a 2 kg rock at a height of 3 m or a 1 kg rock at a height of 6 m?
1. the 2 kg rock
2. the 1 kg rock
3. both the same
4. need more info


PE = mgh.
1 kg rock: PE = 1 kg * 10 m/s^2 * 6 m = 60 J
2 kg rock: PE = 2 kg * 10 m/s^2 * 3 m = 60 J
 
 

2. Which rock will have a greater speed when it hits the ground, a 2 kg rock dropped from a height of 3 m or a 1 kg rock dropped from a height of 6 m?
1. the 2 kg rock
2. the 1 kg rock
3. both the same
4. need more info


If you drop it from higher up, it will be going faster when it hits.
Yes, I know that they both have the same kinetic energy when they hit.  The question asked about speed, not energy.  KE = 0.5 mv^2.  The 2 kg rock has more mass os it must have less v^2 when it hits.
 
 

3. You throw two balls in the air at the same time. They follow the trajectories shown. Ignore air resistance. Which ball hits the ground first?




1. A
2. B
3. both the same
4. need more information


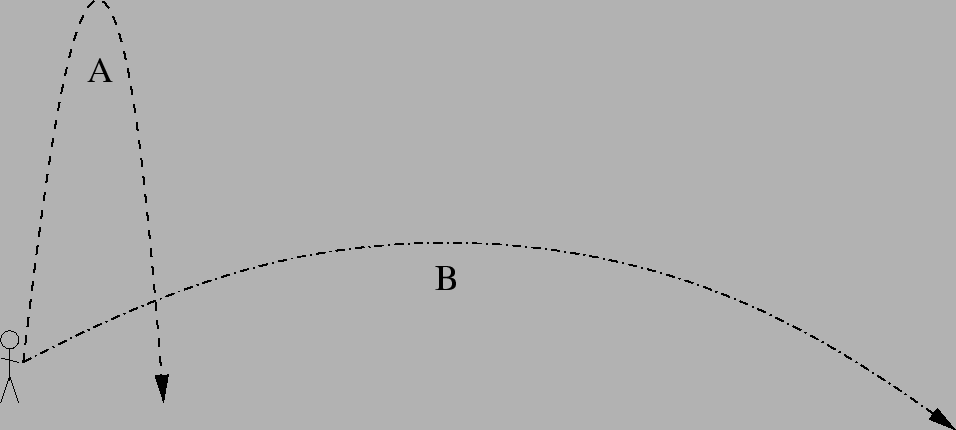
B hits first.  The horizontal speeds are irrelevant so we can make them zero.  In that case, the question becomes: 'If you throw A higher up than B, which one lands first?'  Clearly, the ball that is thrown higher up stays in the air longer.  The answer is thus B lands first.
 

4. My 40 kg son likes to sit on his skate board and be pushed. If I pushed him for a distance of 5 m while applying a horizontal force of 100 N, how much work did I do?


W = F d = 100 N * 5 m = 500 Nm = 500 J
The force and distance  are in the same direction.
 
 

5. In the previous problem, if I push him for 5 m, he will attain a certain speed $v$. If instead I push him for 10 m, his new speed will be (ignoring friction)
1. less than $v$
2. $v$ (ie: the same)
3. between $v$ and $2v$
4. $2v$ (ie: doubled)
5. more than $2v$


If I push him twice as far, I will do twice as much work.  Thus I will double his kinetic energy.  This means that his velocity will increase.  We know that doubling the velocity will quadruple KE so the velocity cannot increase that much.  Thus the answer has to be 'between v and 2v'.
 

6. If the sun doubled its radius from 1 million km to 2 million km without changing its mass, then the gravitational force between the sun and the Earth would
1. increase
2. decrease
3. stay the same
4. need more information


Changing the size of the sun does not change the distance between the center of the sun and the center of the Earth.  Therefore the force will not change.
 
 

7. Norfolk is at a latitude of about 40 degrees N. Our linear speed due to the rotation of the Earth about its axis is about 350 m/s. If you move to the equator your linear speed due to the rotation of the Earth about its axis will
1. increase
2. decrease
3. remain the same
4. need more information


The earth is so large, that if we move around on it, we will not change its rotational velocity significantly.  (We looked at this in a home work problem.)  Therefore rotational velocity is fixed.
The earth rotates around its axis.  The axis passes through the north and south poles.  Therefore, the farther you move from the poles, the farther you are from the axis.  At the equator, you are farthest from the axis and your distance to the axis is equal to the radius of the earth.  Therefore, by moving from Norfolk to the equator, you are increasing the radius of the circle you are moving in.  This means that your linear velocity increases.
 
 

8. A driver of mass 70 kg is driving her red 2000 kg car at 12 m/s. She enters the highway and speeds up to 24 m/s. When she goes from 12 m/s to 24 m/s her kinetic energy
1. halves
2. stays the same
3. doubles
4. quadruples
5. other
You can do this either symbolically:  KE = 0.5 mv^2 -> 0.5 m (2v)^2 = 0.5 m 4 v^2 = 4 * (0.5 m v^2) = 4 times larger
or numerically by plugging in the values for m and v.
 
 
9. A common playground item (in the days before lawsuits) used to be an unpowered merry-go-round. This is a circular platform that is free to rotate. Some children get on the merry-go-round while others push it to make it rotate. Suppose that there are 3 children on it standing near the edge of the platform and it is rotating at 7 revolutions per minute after everyone has stopped pushing. When the children move to the middle of the platform, the rotational speed


 

1. increases
2. decreases
3. remains the same
4. need more information


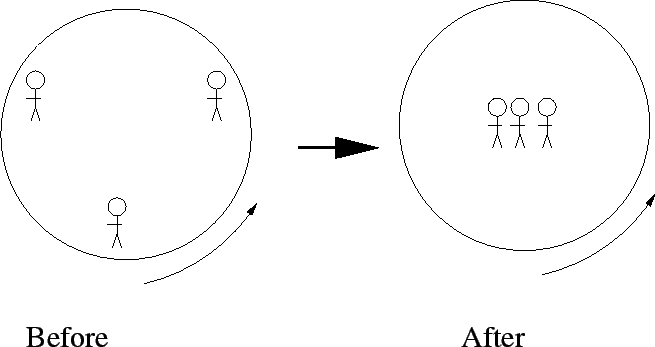
The platform is free to rotate.  This means that once it is spinning, there is no motor to keep it spinning at the same rotational velocity.  It also means that there is no external torque so that angular momentum is conserved.

To get full credit for the problem, you needed to point out that a) angular momentum is conserved, b) that the moment of inertia decreases when the children move closer to the axis, and that therefore c) angular velocity has to increase.
 

10. You throw a 2.3 kg rock horizontally from the top of Mount Trashmore and it hits the ground 75 m away from you and 20 m below you. How much time (in seconds) did it take to fall?


The horizontal velocity is irrelevant.  The only thing that matters is that the rock falls 20 m vertically.  Using d = 1/2 g t^2 we can see that a rock drops 5 m in the first second, and 20 m in the first 2 seconds.  Thus, the answer is 2 s.

Note that falling objects do NOT fall at constant velocity.  You cannot say that because a rock falls 5 m in the first second that it will continue to fall at 5 m/s.  It speeds up.
 
 

11. If I drive my 1000 kg car around a curve at 30 mph, my car needs a certain amount of centripetal force to stay on the curve and not leave the road. If I drive around the same curve at 60 mph, then to stay on the road my car needs
1. less force
2. the same force
3. twice as much force
4. four times as much force
5. need more information


You need a centripetal force of F = mv^2/r to stay on the curve.  If you double v, then you need 4 times as much force.  You can do this either symbolically:
F(30 mph) = mv^2/r -> F(60 mph) = m (2v)^2 / r = m4v^2 / r = 4 (mv^2 / r) = 4 * F(30 mph)
or by choosing some totally arbitrary value for r, plugging in numbers, and seeing what you get.
 
 

12. The tidal force difference of the moon on the Earth is due to the difference in gravitational attraction of the moon on the near side of the Earth and on the far side of the Earth. If the Earth's radius doubled without changing its mass, the tidal force difference on the Earth from the moon would be
1. smaller
2. the same
3. larger
4. need more information


Gravitational force = GMm/R^2
Tidal force = difference in gravitational force = gravitational force on the side of the Earth closest to the moon minus the gravitational force on the side of the Earth farthest from the moon.  If the Earth gets bigger (but the distance from the center of the Earth to the center of the moon stays unchanged), then the distance from the moon to the near side of the Earth gets smaller so the force on the near side of the Earth increases.  Similarly, the distance from the moon to the far side of the Earth gets bigger so the force on the far side of the Earth decreases.  Therefore, the difference between the force on the far side and force on the near side increases, increasing tidal forces.

Alternatively, you can use the equation that tidal force = GMmd/R^3 where d is the size of the Earth and R is the Earth-moon distance.  Increasing d increases the tidal force.

Alternatively, we know that the tidal force on the water in a swimming pool is incredibly infinitesimally tiny because the pool is small.  The tidal force on the water on the Earth is bigger because the Earth is bigger.  Therefore, if we increase the size of the Earth, we increase the tidal force.
 

13. The minimum orbital speed at a distance of 6600 km from the center of the Earth (ie: near the Earth's surface) is 8 km/s. What is the minimum orbital speed at a distance of 10,000 km from the center of the Earth?
1. less than 8 km/s
2. 8 km/s
3. more than 8 km/s
4. need more information


The orbital speed of 8 km/s near the surface of the Earth comes from a) the curvature of the Earth is 5 m in 8 km and b) objects fall 5 m in 1 second.  If we go further from the Earth then  g is smaller so objects fall more slowly.  This means that  it takes more than 1 second to fall 5 m so the minimum velocity is less than 8 km/s.
 
 

14. Normally, you push on the side of a door farthest from the hinges to make it open. If instead, you push on the middle of the door, to apply the same torque to the door (ie: to open it as quickly), you need to apply
1. less force
2. the same force
3. more force
4. need more information


Torque = force times lever arm.  When you reduce the lever arm, you need more force to apply the same torque.
 
 

15. Astronauts in the space shuttle in orbit 250 km above the surface of the Earth appear weightless because
1. the net force on them is zero
2. there is no gravitational pull from the Earth
3. they are above the atmosphere
4. the moon's gravity pulls on them too
5. other


They appear weightless because there is no normal force on them.  Gravity still sucks.
 
 
 
 

16. A box, with its center of mass off center, as indicated by the black dot, is placed on an inclined plane. In which of the four orientations shown, if any, does the box tip over? (You may select more than one.)




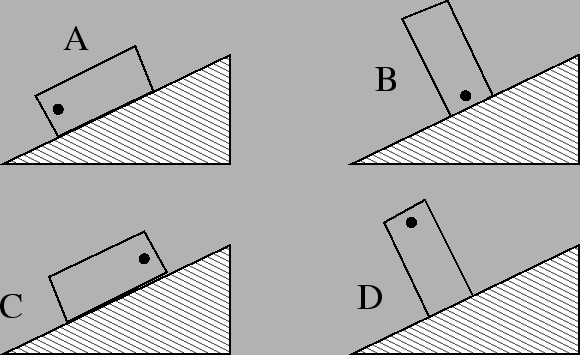
D tips over, A might tip over, B and C are stable.  Draw a line vertically downward from the center of mass.  If it passes through the base of the object, then it is stable.  A vertical line drawn downward from the CoM of D will pass to the left of the base.  It will fall over.  A  vertical line drawn downward from the CoM of A will pass through the leftmost point on the base.