to Name: Honor Code Signature:
Physics 101 Exam 1
6 October 2003 Prof L. Weinstein
There are 19 problems. Please give a short explanation for all multiple choice questions. Show your work for all numerical answers.
- A force of 12 N acts on a
2-kg block for 3 s. What is the acceleration of the block during that
time?
F = ma therefore a = F/m = 12 N / 2 kg = 6 N/kg = 6 m/s^2
2. A 3-kg car travelling at 30 m/s East stops gradually in 6 s. What is the acceleration of the car (give magnitude and direction)?
Delta v
= at therefore a = delta v / t = (-30 m/s East) / 6 s = - 5 m/s^2 East = 5
m/s^2 West
(note
that a negative sign means that it’s going the other way). Since it is slowing down, the acceleration
must be in a direction opposite to the velocity.
3.
Two trains are running on parallel train tracks, each at ![]() mph. You are on one train and your friend is on the other train. You
throw a heavy object directly at your friend. Neglecting air resistance, it
will land
mph. You are on one train and your friend is on the other train. You
throw a heavy object directly at your friend. Neglecting air resistance, it
will land
= 1.4in 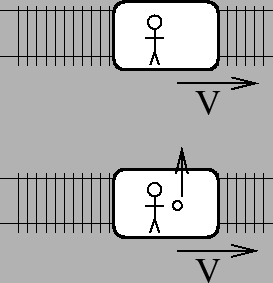
- ahead of your friend
- at
(next to) your friend
- behind your friend
- need more information
Inertia.
All objects have an initial velocity of 30 m/s in the same
direction. There are no forces
that would change that. It’s just
like flipping a coin when sitting on the train. The coin lands in your lap because it has the same
horizontal velocity that you do.
4. What is the average speed of a bicycle if it travels 5 m in the first second, 6 m in the next second, and 7 m in the third second?
speed =
distance traveled / time = 18 m / 3 s = 6 m/s
5. A 3 kg block of ice travelling at a speed of 5 m/s on an icy surface is a attached to a ring by a 2m long string. The string keeps it moving in a horizontal circle. (The left side picture shows the view form the side, the right side picture shows the view from above.) If the string breaks suddenly, which path will the ice block follow?
= 2in 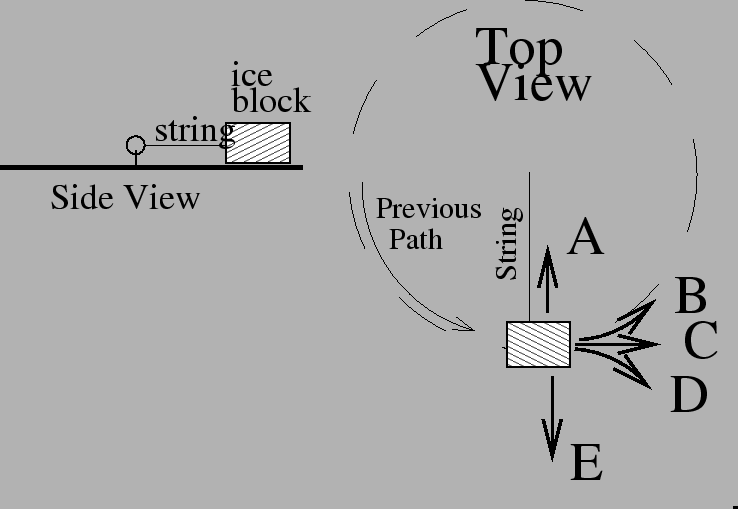
- A
- B
- C
- D
- E
- need more information
Inertia. No forces acting on it means that it travels in a straight
line.
6.
A 4 kg pumpkin falls from the 2nd floor of a building and hits
the ground a time ![]() later. If you want the pumpkin to take twice as
long to hit the ground (ie:
later. If you want the pumpkin to take twice as
long to hit the ground (ie: ![]() ), you should drop it from a
height
), you should drop it from a
height
- 1/4 as high
- 1/3 as high
- 1/2 as high
- twice as high
- four
times as high
- need more information
d = ½ g t^2. If t doubles, than d must increase by a factor of 4. Remember that we calculated this. In 1 second an object fell 5 m and in 2
s it fell 20 m (or 4 times further).
7. A 0.5 kg apple falls from a tree and hits the ground 2 sec later. What was the speed of the apple when it hit the ground?
V = a
t where a = 10 m/s^2 and t = 2 s so that v = (10 m/s^2) * (2 s) = 20 m/s. This is the speed that the apple will
have as it hits the ground.
Many
of you calculated the distance that it fell using d = ½ g t^2 (20 m) and
calculated the speed from speed = distance/time. The problem with this method is that it gives you the
AVERAGE speed for the entire time it was falling, rather than the speed at the
instant it hit the ground.
Remember from the falling spreadsheet that the average speed is ½ of the
final impact speed.
8.
I have three pieces of gold. One has a weight of 1 N on the
Moon (![]() m/s
m/s![]() ). The second has a weight of 1 N
on the Earth (
). The second has a weight of 1 N
on the Earth (![]() m/s
m/s![]() ). The third
has a weight of 1 N on Jupiter (
). The third
has a weight of 1 N on Jupiter (![]() m/s
m/s![]() ). Which piece
has the greatest mass?
). Which piece
has the greatest mass?
- The
one on the Moon
- The one on the Earth
- The one on Jupiter
- need more information
The three pieces of gold are different. You can look at this problem two different ways.
1) F = ma. The force of gravity on each of them is the same (1 N). The acceleration differs. You can use this to calculate m = F/a. Since a is smallest on the moon, m is largest on the moon.
2)
I would weigh the least on the
moon and the most on Jupiter (since my mass doesn’t change). Therefore, if different objects on
different planets have the same weight, the one on the moon must the most mass.
9. The force of friction on a sliding 5 kg chair is 20 N. You push it across the room. How much force do you have to apply once it is moving in order to keep it moving at constant velocity?
- 0 N
- 10 N
- 20
N
- 50 N
- need more information
To move at constant velocity, the total force must be zero. Therefore you need to apply 20 N of force to cancel the 20 N of frictional force from the floor.
In this problem, the chair is already
moving so we do not need to worry about the difference between static and
kinetic friction.
10. I throw a 0.2 kg apple straight up at a speed of 20 m/s. Two seconds later, what are (a) the velocity and (b) the acceleration of the apple?
Each
second the velocity changes by 10 m/s (since g = 10 m/s^2). Since I threw the apple upwards, it’s
speed is decreasing. Therefore
after 1 second its velocity is 10 m/s upwards and after 2 s its velocity is
zero.
The
acceleration does not change. It is
10 m/s^2 downwards.
11. A 1000 kg Honda Civic can go from 0 to 60 mph in 8 sec. When the driver slams on the brakes at 60 mph, it can stop in 4 sec. Which is true?
- The brakes can apply four times as much force on the car as the engine
- The
brakes can apply twice as much force on the car as the engine
- The brakes can apply equally as much force on the car as the engine
- The brakes can apply half as much force on the car as the engine
- The brakes can apply one-fourth as much force on the car as the engine
- Not enough information
Acceleration = velocity change / time. For the engine a = 60 mph / 8 s = 7.5 mph/s. For the brakes, a = 60 mph / 4 s = 15 mph/s or twice as much. Since F = ma and the mass is unchanged, the force must be twice as large.
Most of you got this one correct, but the
explanations were incomplete.
12.
A 4000 kg truck going 30 miles per hour applies the brakes and
stops in a period of time ![]() . If instead the rear brakes fail
so that the brakes only exert half as much force, how much time would it take
to stop?
. If instead the rear brakes fail
so that the brakes only exert half as much force, how much time would it take
to stop?
- one-fourth as much
- half as much
- the same
- twice
as much
- four times as much
- Not enough information
The momentum changes just as much in both cases so you need the same impulse in both cases. When the brakes work you have impulse = force * time. When the force is only half as much, you need twice as much time to have the same impulse.
Alternatively, if the force is reduced by
half, then the acceleration is reduced by half. Then time it takes to change the velocity must double since
delta v = a t.
13. A baseball player slides into homeplate. During the slide, the ground exerts a frictional force on the player that decreases her speed. If this frictional force is the action force, what is the reaction force?
- The force of gravity of the Earth on the player
- The normal force of the ground on the player
- The force of gravity of the player on the Earth
- The
force of friction of the player on the ground
- Other
- Not enough information
Newton’s 3rd Law. The player and the ground interact via
friction.
14. A 2 ton (2000 kg) Ford Explorer travelling at 20 m/s to the right and a 1/2 ton (500 kg) Mini travelling at 20 m/s to the left collide head on and stick together.
Which exerts more force on the other during the collision?
= 0.8in 
- The Explorer exerts more force on the Mini
- The Mini exerts more force on the Explorer
- Both
exert the same force on each other
- Not enough information
Newton’s 3rd Law. The forces are equal and opposite. (Note that the effects of the forces
are not equal!)
15. In the previous problem, what is the speed of the wreckage immediately after the collision (ie: before friction makes them slide to a halt)?
- more than 20 m/s
- 20 m/s
- less
than 20 m/s but not zero
- zero
- Not enough information
By conservation of momentum. The explorer has much more momentum to the right ( p = mv = 2000 kg * 20 m/s = 40,000 kg m/s) than the Mini does to the left ( p = mv = 500 kg * (-20 m/s) = -10,000 kg m/s where I used the minus sign to indicate that it is moving to the left). Thus the total momentum is 30,000 kg m/s (the positive sign indicates that it is moving to the right). The Explorer is slowed by hitting the Mini, but not stopped.
We did this in class with the collision
carts. When the heavier cart hit
the lighter cart traveling at the same speed, the combined carts moved in the
direction of the heavier cart at a slower speed.
16. In the previous problem, in what direction is the wreckage moving immediately after the collision (ie: before friction makes them slide to a halt)?
- right
- left
- up
- down
- They are not moving
- Not enough information
See above explanation.
17. In the previous problem, which car has the greater change in velocity?
- The Explorer
- The
Mini
- Both the same
- Not enough information
There are two ways to look at this:
1) The Mini changes direction so its velocity change is bigger than the Explorer.
2) The force is the same but the Mini’s mass is much smaller so its acceleration (and hence velocity change) must be bigger.
18. In the previous problem, which car has the greater change in momentum?
- The Explorer
- The Mini
- Both
the same
- Not enough information
Same force during collision, same time of
collision, therefore the same impulse is applied to both vehicles.
Therefore the momentum change is the same.
19. A 1 kg flowerpot falls 5 m onto the ground and shatters. What force did the flowerpot exert on the ground?
- 1 N
- 5 N
- 10 N
- 100 N
- Other
- Not
enough information
It falls 5 m, therefore it took 1 s to fall
and hits the ground with a speed of 10 m/s. (We did this in class several times.) However, we do not know how squishy the
ground was, so we do not know how big a ‘crumple zone’ the flower pot had. If it hit concrete, the force would be
really big for a very short time.
If it hit mud, the force would be smaller for a longer period of time.