


Next: About this document ...
to Name: Honor Code Signature:
Physics 101 Exam 2
12 November 2004
Prof L. Weinstein
There are 16 problems. Please give a short explanation for all
multiple choice questions. Show your work for all numerical answers.
Earth's mass
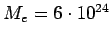 kg kg |
Earth's radius
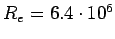 m m |
Moon's mass
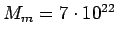 kg kg |
Moon's radius
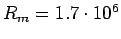 m m |
Sun's mass
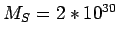 kg kg |
Sun's radius 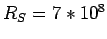 m m |
Earth-Moon distance
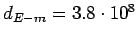 m m |
Earth-Sun distance
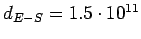 m m |
G =
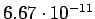 N N m m /kg /kg |
|
- You throw a 2-kg block upward at an angle of 45
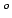 and a speed of
6 m/s toward your friend. What is its kinetic energy as it leaves
your hand?
and a speed of
6 m/s toward your friend. What is its kinetic energy as it leaves
your hand?
- You throw a 3-kg block upward at an angle of 37
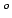 with a kinetic
energy of 24 J toward your friend. What is its kinetic energy immediately
(ie: a split second) before your friend catches it? (Assume that
your friend catches it at the same height that you threw it from.
Ignore air resistance.)
with a kinetic
energy of 24 J toward your friend. What is its kinetic energy immediately
(ie: a split second) before your friend catches it? (Assume that
your friend catches it at the same height that you threw it from.
Ignore air resistance.)
= 0.5in

- Aircraft carriers use catapults to rapidly accelerate airplanes
to high enough speeds that they can remain airborne. (Airplanes crash
if they fly too slowly.) Assume the catapult can do a fixed amount
of work on each airplane. If the catapult can give a plane with
mass
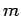 an initial speed
an initial speed 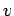 , how much speed can the catapult give a
lighter plane with mass
, how much speed can the catapult give a
lighter plane with mass 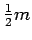 ?
?
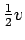
- between
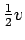 and
and 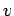
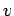
- between
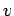 and
and 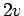
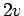
- need more information
- You compete in the pumpkin dropping competition and build a 1-m
tall pumpkin catcher that successfully catches (without breaking) a
4-kg pumpkin dropped from a 10-story building. If a new competition
is held where the pumpkin is dropped from a 20-story building, how
tall should your new pumpkin catcher be in order to successfully
catch the pumpkin? (Assume that the new pumpkin catcher is built just
like the old one, except for its size. Ignore air resistance.)
- 1/4 m
- 1/2 m
- 1 m
- 2 m
- 4 m
- need more information
- When you drive your car one mile at a speed of 30 mph, the
tires of your car make a certain number of rotations. Next you
test drive a new vehicle with tires twice the diameter of your
car's tires. How many rotations do these tires make in one mile?
- 1/4 as many
- half as many
- the same
- double
- quadruple
- need more information
- Norfolk is at a latitude of about 40 degrees N. Our linear speed
due to the rotation of the Earth about its axis is about 350 m/s. If
you move to the equator your linear speed due to the rotation of the
Earth about its axis will
- decrease
- stay the same
- increase
- need more information
- A favorite playground item is a large horizontal tire held up by
chains. The tire is free to swing and also to rotate. Let's
just consider the rotational motion. Ignore friction. The pictures
show the swing as viewed from above. Two children
of about equal mass get on the swing and sit up straight (the
left-hand picture). Their parents start the swing rotating at some
rotational speed. If the children now lean way out (the right-hand
picture), the rotational speed of the swing will
= 1.5in
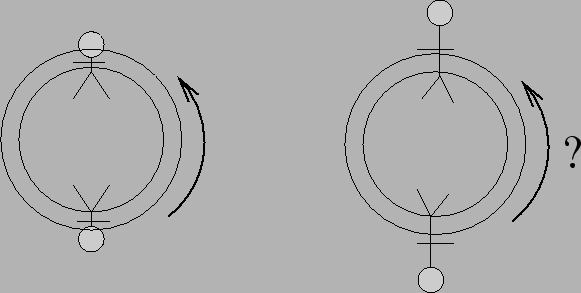
- decrease
- stay the same
- increase
- need more information
- In order to be in Low Earth Orbit (ie: about 200 km from the
surface of the Earth or about 6600 km from the center of the Earth),
you need to have a tangential speed of 8 km/s. If the Earth
expands so that it has the
same mass but twice the radius, what speed would you need to be in
Low Earth Orbit 200 km above the (expanded) surface?
- less than 8 km/s
- 8 km/s
- more than 8 km/s
- need more information
- Calculate the gravitational force between the Earth and the Sun (see
the numbers at top of exam).
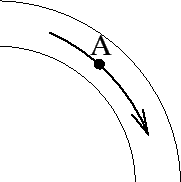
- You drive your car on the curved highway exit ramp at 20 mph.
In order for your car to follow the curve and stay on the road, you
need 2,000 N of frictional force.
a) draw an arrow showing the direction of the frictional force when
the car is at point  .
.
b) How much force will you need to
follow the curve and stay on the road if you drive on the same curve
at 60 mph?
= 1.5in
- If you moved to another planet with twice the mass of the Earth
but the same radius, the acceleration due to gravity at the surface
would be
- four times smaller than Earth's (ie: 2.5 m/s
 )
)
- two times smaller than Earth's (ie: 5 m/s
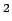 )
)
- the same as Earth's (ie: 10 m/s
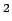 )
)
- two times larger than Earth's (ie: 20 m/s
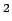 )
)
- four times larger than Earth's (ie: 40 m/s
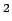 )
)
- need more information
- (no explanation needed) When you accelerate your standard (ie:
non-hybrid) gasoline-powered car from 0 to 60 mph, you are
converting chemical energy in the gasoline to kinetic energy (and
other forms of energy). When you use your brakes to stop, what form
of energy is the kinetic energy converted to?
- chemical
- potential
- thermal (ie: heat)
- other
- need more information
- You throw a 7-kg rock with an initial speed of
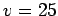 m/s such that
its horizontal speed is 15 m/s and its vertical speed is 20 m/s.
How much time is the rock in the air? Ignore air resistance.
Assume the rock lands at the same height that you threw it from.
m/s such that
its horizontal speed is 15 m/s and its vertical speed is 20 m/s.
How much time is the rock in the air? Ignore air resistance.
Assume the rock lands at the same height that you threw it from.
= 1.5in
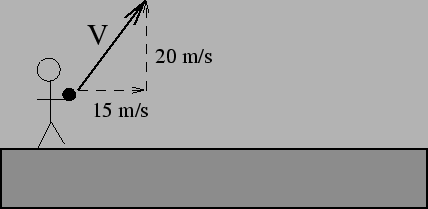
- Olympics divers need to rotate their bodies a certain number of
times for specific dives. At the beginning of the dive, a diver's
body is typically fully extended and she is rotating at a certain
rate. When the diver 'tucks' (ie: draws her legs up to her chest
and brings her arms in), will she rotate faster or slower than when
her body is extended?
= 1.1in
- faster (more rotations per second)
- same rotational speed
- slower (fewer rotations per second)
- need more information
- You jump out of an airplane and are in free fall. While you are
falling, you take out a cup and a bottle of water. You tilt the
bottle in order to pour the water from the bottle into the cup.
Ignore air resistance. What happens?
- the water pours normally
- the water pours faster than normal
- the water pours slower than normal
- the water does not pour (it stays in the bottle)
- need more information
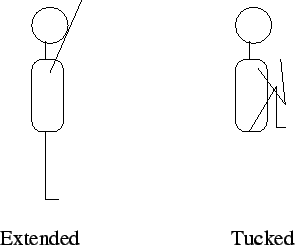
- In one of the Star Trek movies, Captain Kirk falls off of a high
cliff. If he hit the ground, he would die. Fortunately, Mr. Spock
swoops in horizontally with his aircar and saves Kirk by catching
him about 6 inches from the ground. Would this work in real life?
= 1.1in
- yes
- no
- need more information



Next: About this document ...
2004-11-16


![]() .
.



