to Name: Honor Code Signature:
There are 16 problems. Please give a short explanation for all multiple choice questions. Show your work for all numerical answers.
G =
![]() N
N![]() m
m![]() /kg
/kg![]()
Earth's mass
![]() kg
kg
Earth's radius
![]() m
m
Moon's mass
![]() kg
kg
Moon's radius
![]() m
m
Earth-Moon distance
![]() m
m
Earth-Sun distance
![]() m
m
closest Earth-Jupiter distance
![]() m
m
Jupiter's mass
![]() kg
kg
30 Joules. It starts with PE = 0 and KE = 30 J. At the peak of the trajectory, it has PE = 30 J and KE = 0 J. This is because a) energy is conserved and b) at the peak the block is not moving so it has zero velocity and zero KE.
![]() so that when you double the mass, you double the
KE needed to go 30 m/s.
so that when you double the mass, you double the
KE needed to go 30 m/s.
There are two parts to this solution: 1) when you double ![]() , KE
quadruples since
, KE
quadruples since ![]() , and 2) to stop the car, you need to
do work
, and 2) to stop the car, you need to
do work ![]() equal to the change in KE (
equal to the change in KE (
![]() . Since you need to do 4 times the work and the force
exerted is the same, you will need four times the distance.)
. Since you need to do 4 times the work and the force
exerted is the same, you will need four times the distance.)
Momentum has a direction. This means that
if half the group is walking to the left and the other half is walking
to the right, their total momentum can be zero. More technically,
momentum is a vector:
![]() .
.
KE does not have a direction. It is always positive. (Since KE =
1/2mv^2. When you square the ![]() , minus signs become positive and
there is no direction anymore.)
, minus signs become positive and
there is no direction anymore.)
Therefore total momentum can be zero but total kinetic energy cannot be zero.
Many of you wrote that if velocity was constant then momentum could be zero. This is wrong. If velocity is constant, then momentum is not changing and therefore the change in momentum is zero. This does not mean that momentum itself is zero.
Rotational speed measures the number of rotations made per
second. Linear speed measures the number of meters travelled in that
time. You start out covering a distance of ![]() in 2 s. Then it
speeds up and you cover the same distance in half the time. You have
doubled your speed.
in 2 s. Then it
speeds up and you cover the same distance in half the time. You have
doubled your speed.
Note that the radius of the LP did not change.
An astronaut is in the centrifuge as it rotates around. She has a
linear speed ![]() and feels a centripetal force from the centrifuge.
If her linear speed doubles, then the force on her from the centrifuge
will
and feels a centripetal force from the centrifuge.
If her linear speed doubles, then the force on her from the centrifuge
will
Centripetal force ![]() . If you double
. If you double ![]() then
then ![]() will quadruple.
will quadruple.
![]() . Quadruple height and PE will quadruple.
. Quadruple height and PE will quadruple.
You need a centripetal force to go in a circle. If there is no force, then you will go in a straight line. (Try rounding a curve at high speed on an icy day. You won't make it. On second thought, don't try it.) If the force is directed forward, then you will go faster but you won't change direction.
If the moon was not moving, then Earth's gravity would pull it toward the Earth and there would be a horrible crash. The large tangential velocity makes the moon miss the Earth.
If there was no net force on the moon, then it would travel in a straight line and leave us forever.
The Earth's gravity still pulls on the moon. The Earth's pull is weaker that far away, but it is still very strong and keeps the moon in orbit.
The pull of the sun and the planets does not significantly affect the orbit of the moon around the Earth.
![]() where
where ![]() is the gravitational constant,
is the gravitational constant, ![]() and
and
![]() are the masses of the two objects that are pulling on each other
(in this case the baby with
are the masses of the two objects that are pulling on each other
(in this case the baby with ![]() kg and Jupiter with
kg and Jupiter with
![]() kg), and
kg), and ![]() is the distance between them (in this
case
is the distance between them (in this
case
![]() m). Thus:
m). Thus:
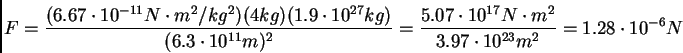
![]() You are now twice as far from the center of
the planet so
You are now twice as far from the center of
the planet so ![]() doubles and
doubles and ![]() gets four times smaller.
gets four times smaller.
= 1.5in
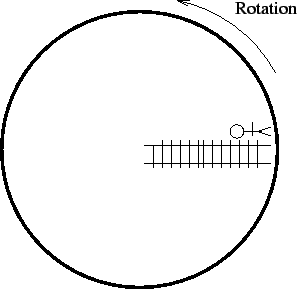
There are no external torques on the space habitat. Therefore angular momentum is conserved. When you move to the center of the habitat, you decrease the total rotational inertia of the habitat. Therefore, the rotational speed of the habitat increases. This is just like the ice skater bringing her arms in and spinning faster or the student on the rotating stool who rotated faster when she brought her arms (and the weights) in and rotated slower when she held her arms (and the weights) out.
The farther the mass is from the center of rotation, the harder
it is to make it rotate and greater its rotational inertia. In
equation terms, ![]() . The foot of the straight leg is farther
from the axis of rotation (the hip) so the straight leg has larger
rotational inertia.
. The foot of the straight leg is farther
from the axis of rotation (the hip) so the straight leg has larger
rotational inertia.
When you run, you bend your leg to decrease its rotational inertia so you can bring it forward faster to take the next step.
Torque = force times lever arm. Both brakes apply the same force. The one that has the larger lever arm will be more effective at stopping the bike.
The rim brakes apply their force far from the axle. This means that there is a large lever arm. The hub brakes apply their force very close to the axle. This means that there is a short lever arm. This is exactly the same physical situation as pushing on a door. You want to push on the door as far from the axis of rotation (the hinges) as possible. This is why the door knob is not next to the hinges.
The horizontal speed is irrelevant. This is identical to
dropping a rock and asking how far it falls in 2 s. The distance it
falls is ![]() where
where ![]() . Thus
. Thus
Energy is conserved. The energy to run the car comes from the gasoline. The air conditioner uses energy that comes from burning gasoline. This means that you will not be able to travel as far on 1 gallon of gas. Note that this probably changes your mileage by about 1 mpg.
When the moon was closer, the gravitational force on the Earth
was larger since ![]() . But this is not enough, since the
tides depend on the difference between the gravitational force of the
moon on the Earth at the near side of the Earth and at the center of
the Earth. This difference (and hence the tidal forces and hence the
height of the tides) also increases. There are two ways to justify
this: a: use the ugly equation: Tidal force =
. But this is not enough, since the
tides depend on the difference between the gravitational force of the
moon on the Earth at the near side of the Earth and at the center of
the Earth. This difference (and hence the tidal forces and hence the
height of the tides) also increases. There are two ways to justify
this: a: use the ugly equation: Tidal force =
![]() or b: The moon exerts more tidal force on the
Earth than the Sun does because the moon is much closer to the Earth
than the Sun. Therefore, if the moon was even closer, the tides would
be even bigger.
or b: The moon exerts more tidal force on the
Earth than the Sun does because the moon is much closer to the Earth
than the Sun. Therefore, if the moon was even closer, the tides would
be even bigger.