F = ma, therefore m = F/a = 18 N / 3 m/s^2 = 6 kg (since 1 N = 1 kg m/s^2)
a) What was the change in velocity of the car during that time?
b) What was the acceleration of the car during that time (give magnitude and direction)?
a) Let's take East as + and
West as -. Then the velocity went from +38 m/s to -27 m/s.
delta v = v_final -
v_initial = -27 m/s - (+38 m/s) = -65 m/s = 65 m/s West.
b) a = delta v / t = 65 m/s
West / 5 s = 13 m/s^2 West
If you got part (a) wrong, I
used that as the starting point for part (b).
You are travelling in a golfcart down the road at a speed of 10 m/s. You want to throw your full water bottle to your friend, who is standing still. You throw the water bottle as you pass your friend. Neglect air resistance. To make sure that she can catch it, you should aim your throw:
= 1.4in
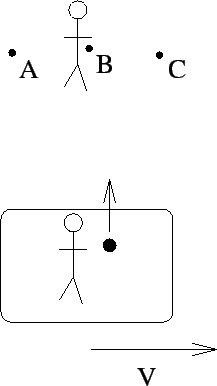
- at point A (behind your friend)
- at point B (at your friend)
- at point C (ahead of your friend)
- need more information
The bottle keeps its horizontal velocity. Therefore you have to aim it behind your friend at point A. (The layout of this question was confusing to many people so I made it extra credit.)
v_average = total
distance / total time = (10+60+50 miles) / 3 hours = 40 miles/hour
Because there are no forces acting on
your car, it goes in a straight line at constant speed. I took
off 5 points for a straight line in the wrong direction.
- 1/4 as high
- 1/3 as high
- 1/2 as high
- twice as high
- four times as high
- need more information
Oops. This is really an energy question. I deleted it from the test.
d = (1/2)gt^2
2d/g = t^2
sqrt(2d/g) = t
sqrt((2*20 m)/(10 m/s^2)) = t
sqrt(4 s^2) = t
t = 2 s.
Note that you get the number 2 by the incorrect method where you divide the distance (20 m) by the acceleration (10 m/s^2) to get 2. This gives the wrong units (s^2).
- 0 N
- between 0 and 1500 N
- 1500 N
- more than 1500 N
- need more information
The car is moving with constant speed in a straight line, therefore velocity is constant, acceleration is zero and the net force on the car is zero.
0 = F_net = F_engine + F_air_and_friction
Therefore F_air_and_friction must be equal and opposite to F_engine, or 1500 N.
This is NOT a 3rd law problem. We did this in class on a quiz question.
The height and mass of
the ball are irrelevent. The velocity is 20 m/s down. After
one second it has increased by 10 m/s (since g = 10 m/s^2) so it is 30
m/s. After 2 s, it is 40 m/s.
The acceleration is 10 m/s^2
(gravity is gravity).
We did this in class on a
quiz question.
- 2 sec
- 4 sec
- 8 sec
- 16 sec
- 32 sec
- Not enough information
The force is unchanged. The mass is unchanged. Therefore the acceleration is unchanged. Therefore the time to accelerate is unchanged.
Gravity exerts a vertical force on the car. This does not affect the horizontal forces and accelerations. We did this in class and on the homework.
- one-fourth as much
- half as much
- the same
- twice as much
- four times as much
- Not enough information
In both cases, it has to change speed from 45 mph to zero. When the roads are dry, it has a_dry = F/m. When the roads are wet, a_wet = F_wet/m = (F/2)/m = (1/2)a_dry. Therefore the acceleration is half as large. Since a = v/t, we know that t = v/a. If a is half as large, we will need twice as much time to change the velocity by the same amount.
Alternatively, we have to apply an impulse Ft to change the momentum from (1000 kg)(45 mph) to 0. If F is half as large, t must double to compensate.
I was looking for arguments as to a) why t needed to be larger and b) why it needed to be two times larger, not four times.
- gravity pulling on the air
- the air pushing on you
- the air pushing on the fan
- gravity pulling on the fan
- gravity pulling on you
- Other
- Not enough information
Which exerts more force on the other during the collision?
- The big hockey player exerts more force on the small hockey fan
- The small hockey fan exerts more force on the big hockey player
- Both exert the same force on each other
- Not enough information
Newton's third law. (That's all the explanation I needed.) The fan and the player interact. Therefore the force exerted on the player equals the force exerted on the fan. This is just like in class where we looked at lots of different collisions and interactions.
Another acceptable explanation is: 'Same force, different results'
- more than 12 m/s
- 12 m/s
- less than 12 m/s but not zero
- zero
- Not enough information
Conservation of momentum. Before we have 100 kg moving at 12 m/s (and 50 kg not moving), now we have more mass so the speed must decrease.
- The big player
- The small fan
- Both the same
- Not enough information
Same force, different mass. a = F/m. The person with the smaller mass will have the larger acceleration. You could also calculate it exactly. The speed before was 12 m/s and afterwards it was 8 m/s (in the same direction). Therefore the small fan had the larger change in velocity.
- The big player
- The small fan
- Both the same
- Not enough information
Same force of collision, same time of collision, therefore they each had the same impulse and thus the same momentum change. Another way to look at it is that momentum was conserved. Therefore, if the momentum of one person increased, the other had to decrease by the exact same amount to compensate. We did this entire collision problem in class (with two cars colliding) and also on the homework (also with two cars colliding).
- 0.75
- 1.5
- 5
- 8.25
- 55
- other
- Not enough information
To get the force, we need to know the time. Ft = delta(p). We know the change in momentum; we don't know the time.
Alternatively, we can use F = ma = m delta(v)/t. We know m and the change in velocity; we don't know the time. We did a problem just like this in class (with the rocket sled).
gravity is gravity. The only force on the rock is gravity. F = mg = 1 kg * 10 m/s^2 = 10 N.
- more than the person's weight
- equal to the person's weight
- less than the person's weight
- Not enough information
If the elevator was standing still (or moving at constant velocity), then you would not be accelerating. Thus the total force on you would be zero so that the normal force (from the elevator) would equal the force exerted on you by gravity (your weight).
However, the elevator is accelerating upward. To make this happen, the total force on you must be upwards so that F_normal must be greater than F_gravity. This was a homework problem (about jumping).
So many of you misunderstood this problem that I made it extra credit.