Physics 101 Exam 1
4 October 2002 Prof L. Weinstein

There are 16 problems. Please give a short explanation for all multiple choice questions. Show your work for all numerical answers.
 
 

  1. The Voyager 1 spacecraft was launched from the Earth in 1977 and is now 12.4 billion km from the Earth. What keeps the spacecraft going after the rocket no longer pushes it?

    2.  

     

    Inertia.  There are no significant forces on the spacecraft, therefore by Newton's 1st Law, its velocity does not change much.

    Gravity does extend into outer space (as we will learn in chapter 9).

    'Momentum' gets 1/2 credit.  'Inertia' or 'Newton's 1st Law' gets full credit.
     
     
     

  2. You are on a sailing ship traveling at a constant velocity of 5 m/s. You drop a 1 kg iron block from the top of the 20 m high mast. Where does the block land?

    3.  

     

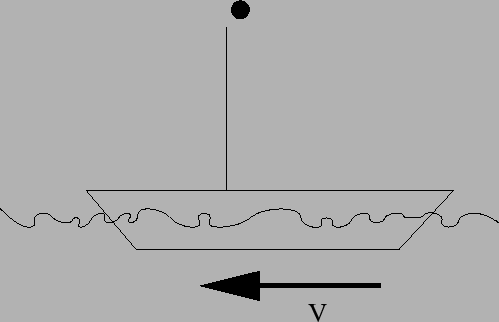
    \epsffile{boat.ps}

    1. 5 m in front of the mast
    2. at the base of the mast
    3. 5 m behind the mast
    4. 10 m behind the mast
    5. Not enough information


    At the base of the mast.  Both the iron block and the ship have the same horizontal velocity so, as viewed from the ship, the block drops straight down.
     

  3. For every force, there exists an equal and opposite force. Consider a rock dropped from a tall building. If the action force is that of the Earth pulling down on the rock, what is the reaction force?

    4.  

     

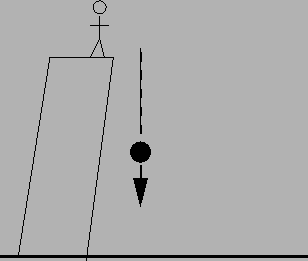
    \epsffile{droprock.ps}
    The reaction force is the rock pulling up on the Earth.
     
     

  4. A 1 kg rock is thrown straight upward with a speed of 30 m/s. Neglecting air resistance, what is the net force on the rock when it is halfway down from the top of its path?

    5.  

     

    Gravity is gravity.  F = ma = 1 kg * 10 m/s^2 = 10 N
     

  5. A 350 lb football player and a 94 lb gymnast pull on opposite ends of a rope in a tug-of-war. Who exerts the greatest force on the rope?
    1. the football player
    2. the gymnast
    3. both forces are the same
    4. Not enough information


    Newton's 3rd Law.  (The forces are the same but the effects will be different!)
     
     

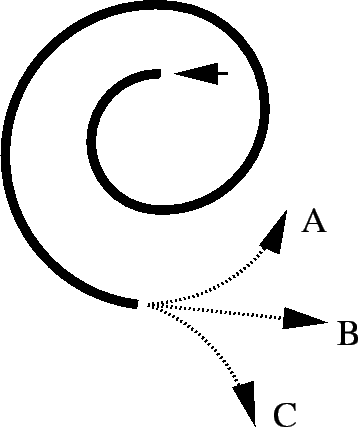
  6. You are looking down on a spiral tube from above as it sits on a flat table. A pellet is fired into the spiral tube at the arrow in the center. When it emerges, which path will it follow (ignore gravity)?

    7.  

     

    \epsffile{spiral.eps}

    1. A
    2. B
    3. C
    4. Not enough information


    No forces -> no acceleration -> the object continues in straight line motion at the same speed.  The answer is B.
     
     

  7. The Levi-Strauss trademark shows two horses trying to pull apart a pair of pants. Suppose that Levi had only one horse and attached the other side of the pants to a fencepost. Using only one horse would

    8.  

     

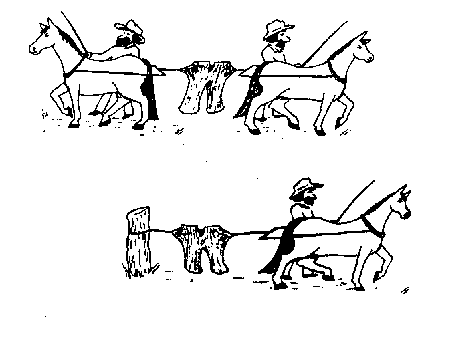
    \epsffile{pullapart.ps}

    1. reduce the tension on the pants by one-half
    2. not change the tension on the pants
    3. double the tension on the pants
    4. other
    5. Not enough information


    We did this in class with the scale and two weights.  The reading on the scale did not change when we had one weight pulling from each side or when we had one weight pulling from one side and the other side held fixed.

    The reason is Newton's 1st Law.  The pants are not moving.  This means that the net force on the pants is zero.  This means that the force of the first horse is exactly counterbalanced by the second horse and it is also exactly counterbalanced by the post.  Thus, the tension in the pants does not change.

    It has nothing to do with Newton's third law.  If the stump was replaced by a small twig, then the tension on the pants would be much less (since the twig [and pants] would be accelerating) but Newton's third law would still apply.
     

  8. You throw a 1.3 kg ball straight up in the air. It lands next to you 4 seconds later. Assume the ball spends half the time going up and the other half falling down. Ignore air resistance. How high did the ball go?

    9.  

     

    It takes 2 s to go up.  d = 1/2 g t^2 = (1/2) (10m/s^2)(2 s)^2 = 20 m.

    If you put in 4 s, you got 80 m.  Note that doubling the time quadruples the distance.  I only took off 3 points for this.
     
     

  9. A 4000 kg truck going 30 miles per hour applies the brakes and stops in a certain amount of time. If you double the mass of the truck and the brakes apply the same amount of force, how much time will it take to stop?
    1. half as much
    2. the same
    3. twice as much
    4. four times as much
    5. Not enough information


    To get full credit for the explanation, you need to point out two things:  1) doubling the mass while keeping the force constant halves the acceleration (since F = ma) and 2) since delta v = at, to get the same change in velocity with half the acceleration you need twice the time.

    You can also point out that 1) the momentum (p= mv) has doubled, 2) therefore the impulse = Ft must double, 3) therefore t must double.
     
     

  10. A 4000 kg truck going 30 miles per hour applies the brakes and stops in a certain amount of time. If the truck is travelling at 60 miles per hour and the brakes apply the same amount of force, how much time will it take to stop?
    1. half as much
    2. the same
    3. twice as much
    4. four times as much
    5. Not enough information


    To get full credit for the explanation, you need to point out two things:  1) the acceleration is unchanged (since F = ma) and 2) since delta v = at, to get twice the  change in velocity with  the same acceleration you need twice the time.

    You can also point out that 1) the momentum (p= mv) has doubled, 2) therefore the impulse = Ft must double, 3) therefore t must double.
     
     

  11. A car rounds a curve while maintaining a constant speed. Is there a non-zero net force on the car as it rounds the curve?
    1. No
    2. Yes
    3. It depends on the sharpness of the curve and the speed of the car
    4. Not enough information


    Your direction is changing, therefore your velocity is changing, therefore there is an acceleration, therefore there is a force.

    If there is no force, you will go in a straight line, not a curve.

    Many of you thought constant 'speed' meant constant 'velocity'.  It does not.  Velocity is speed with a direction.

    Some of you were confused by the term 'non-zero'.  If you showed that you understood the physics, I gave you full credit.
     
     
     
     

  12. An 83 kg batter hits a 150 g baseball travelling toward him at 40 m/s. After being hit, the ball is travelling at 35 m/s away from him. Assume that the impact took 0.002 seconds.

    13.  

     

    a) What was the acceleration of the ball during the impact?

    a = change in velocity / time
    change in velocity = 40 m/s toward - 35 m/s away = 75 m/s
    a = 75 m/s / 0.002 s = 37,500 m/s^2 = 3.75 * 10^4 m/s^2
    rather a lot!

    I took off 3 points for the wrong change in velocity.  I took off one point for the wrong units on acceleration.

    b) What impulse did the ball exert on the bat during the impact?

    This problem was too hard.  I counted it as extra credit.

    The impulse of the ball on the bat is equal to and opposite the impulse of the bat on the ball:

    I = delta p = m delta v = 0.15 kg * 75 m/s = 11.25 kg m/s
    you can also get this from the force:
    I = Ft = (ma)t= 0.15 kg * (3.75*10^4 m/s^2) * 0.002 s

    c) What force did the bat exert on the ball during the impact?

    This problem was too hard.  I counted it as extra credit.

     F = ma = 0.15 kg * 3.75 * 10^4 m/s^2 = 5.625 * 10^3 N
    or you can get this from the impulse
    F = I/t = 11.25 kg m/s / 0.002 s

    Note that the acceleration and the force are very large because the collision happens in such a short period of time.
    Note also that the acceleration occurs DURING the impact because it is while the bat is hitting the ball that the velocity of the ball changes.
     

  13. An airplane flies 600 km in a straight line from Virginia Beach to New York City in 5 hours. What was its average speed? (Don't forget the units.)

    14.  

     

    v = distance / time = 600 km / 5 hr = 120 km/hr

    answers in other units are also OK.
     
     

  14. A 727 airplane has a mass of 70 tons ($7\times 10^4$ kg). In an airplane pulling competition, teams of 20 people compete to pull the airplane a distance of 4 m. An average time is 10 s.

    15.  

     

    a) What was the average speed of the airplane?

    v_average = distance / time = 4 m / 10 s = 0.4 m/s

    b) Assume the maximum speed was twice the average speed. What was the acceleration of the airplane?

    delta v = final velocity - initial velocity  = 0.8 m/s - 0 m/s = 0.8 m/s

    a = delta v / t = 0.8 m/s / 10 s = 0.08 m/s^2

    They're pulling hard but the plane is not accelerating much!

    c) What force did the team of people exert on the airplane?

    F = ma = 7*10^4 kg * 0.08 m/s^2 = 5.6*10^3 N
     

  15. You are sliding along a frictionless icy pond at 6 m/s. You collide with a friend standing on the slippery ice and grab onto him. Your combined speed is now
    1. 0
    2. less than 6 m/s but more than 0
    3. 6 m/s
    4. more than 6 m/s but less than 10 m/s
    5. 10 m/s
    6. Not enough information


    Momentum is conserved.  This is an inelastic collision.  When you hit somebody standing still you slow down and he speeds up.  You don't stop because there are no outside forces on you.
     
     

  16. In the previous problem, if your mass is 50 kg and his mass is 100 kg, what is your combined speed after the collision?

    17.  

     

    momentum before = momentum after
    P_before = 50 kg * 6 m/s + 100 kg * 0 = 300 kg m/s
    P_after = (50 kg + 100 kg) * v_after
    v_after = 300 kg m/s / 150 kg = 2 m/s


2002-10-07