Scientific Machine Learning

This line of research focuses on the development of data-driven approaches for latent dynamics discovery in complex systems. This involves leveraging machine learning (ML)/AI techniques to uncover hidden dynamics in high-dimensional datasets and understanding the underlying structures. Publications can be found on google scholar

key topics include:

• Dynamics Learning
• Data-driven latent space discovery
• Generative AI models
• Applications in physical and engineering systems

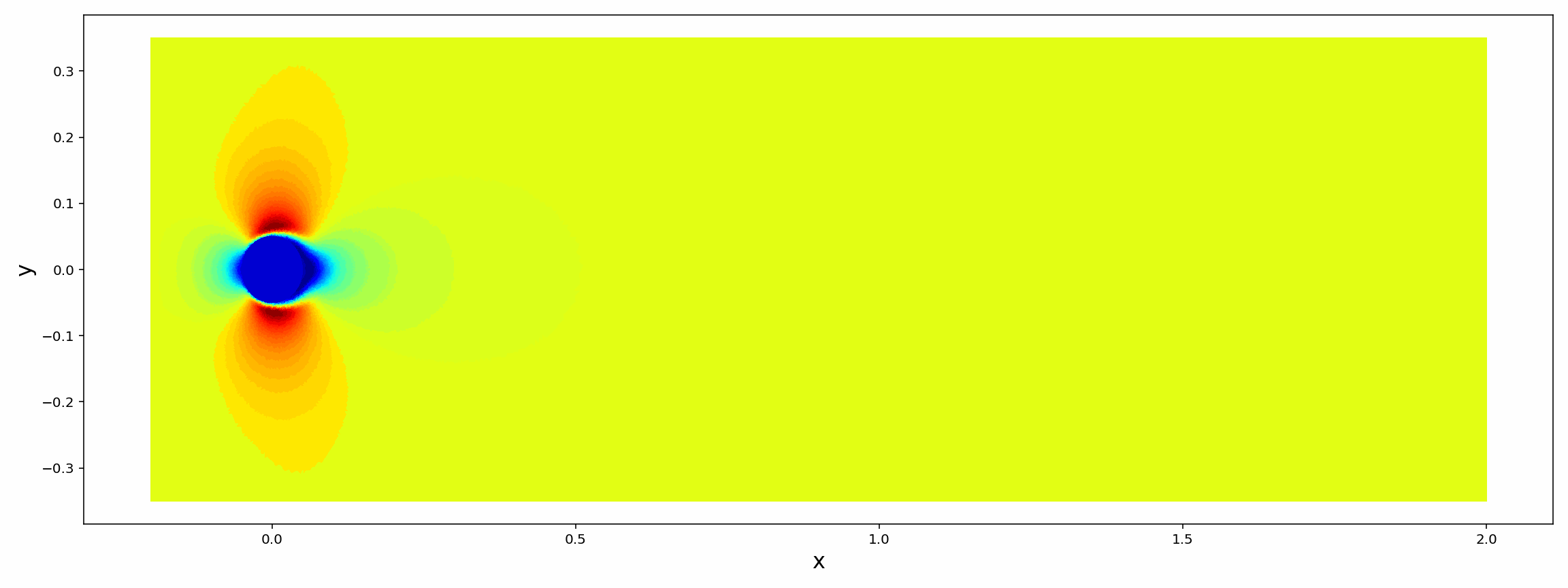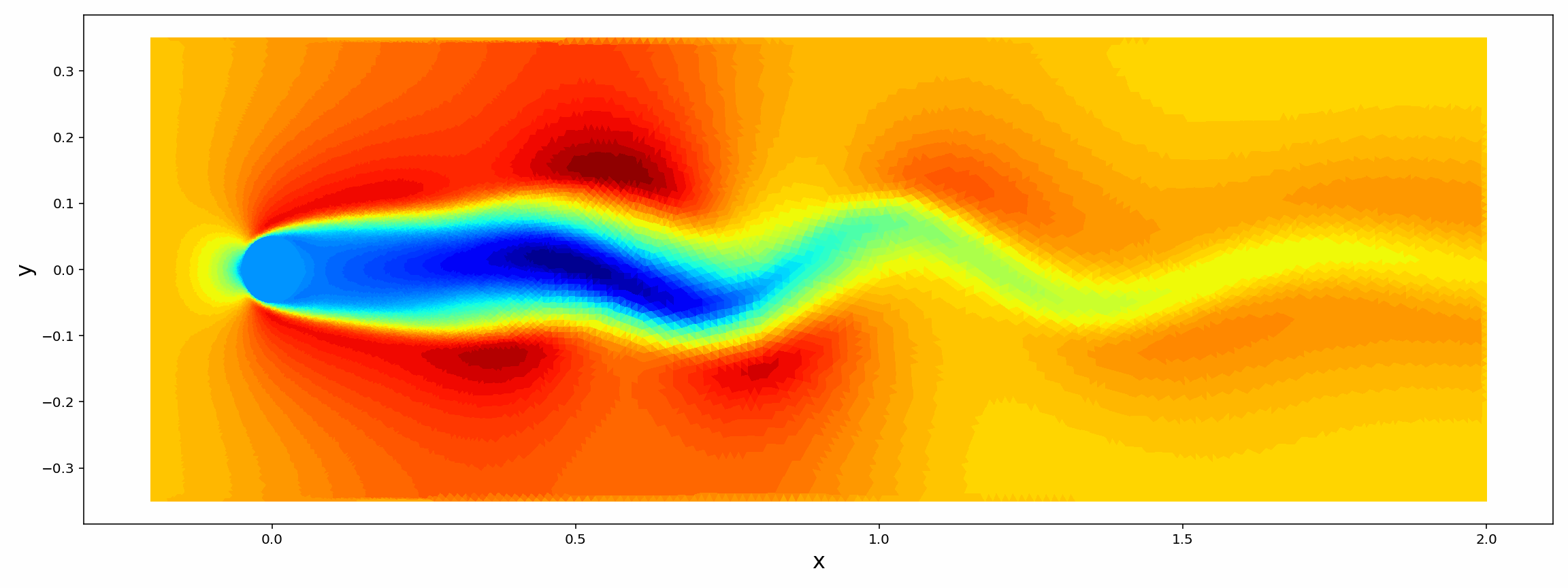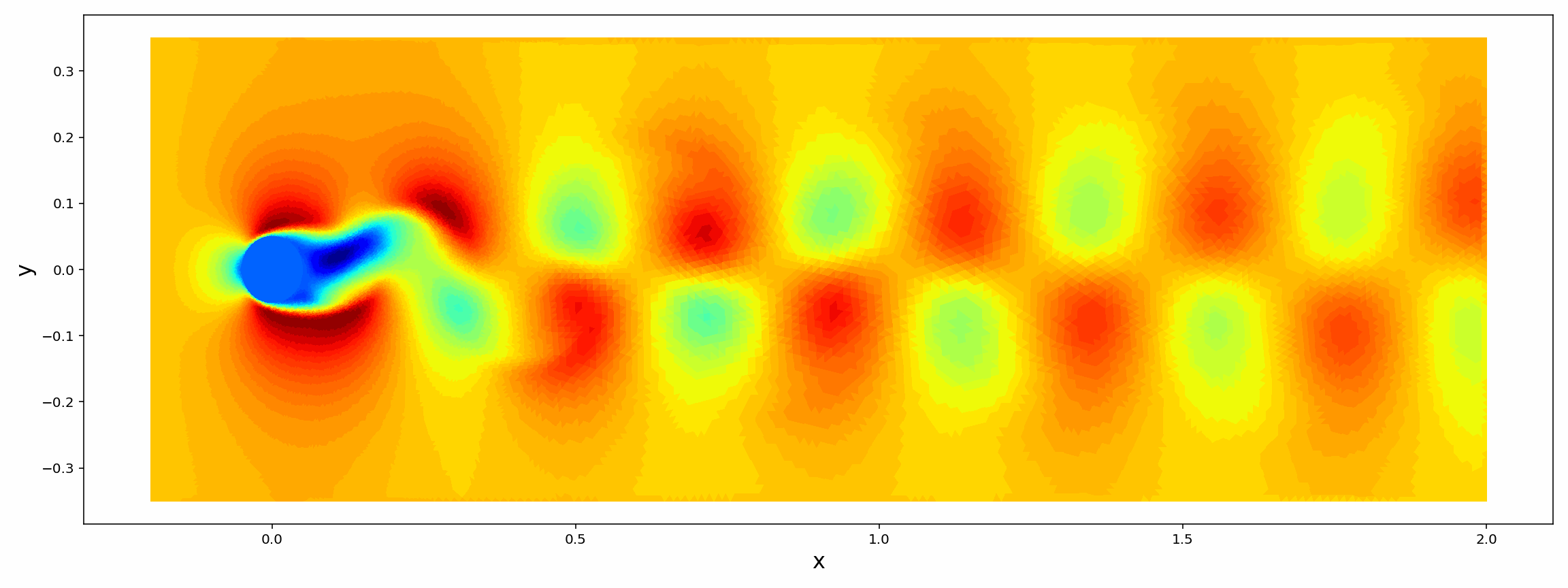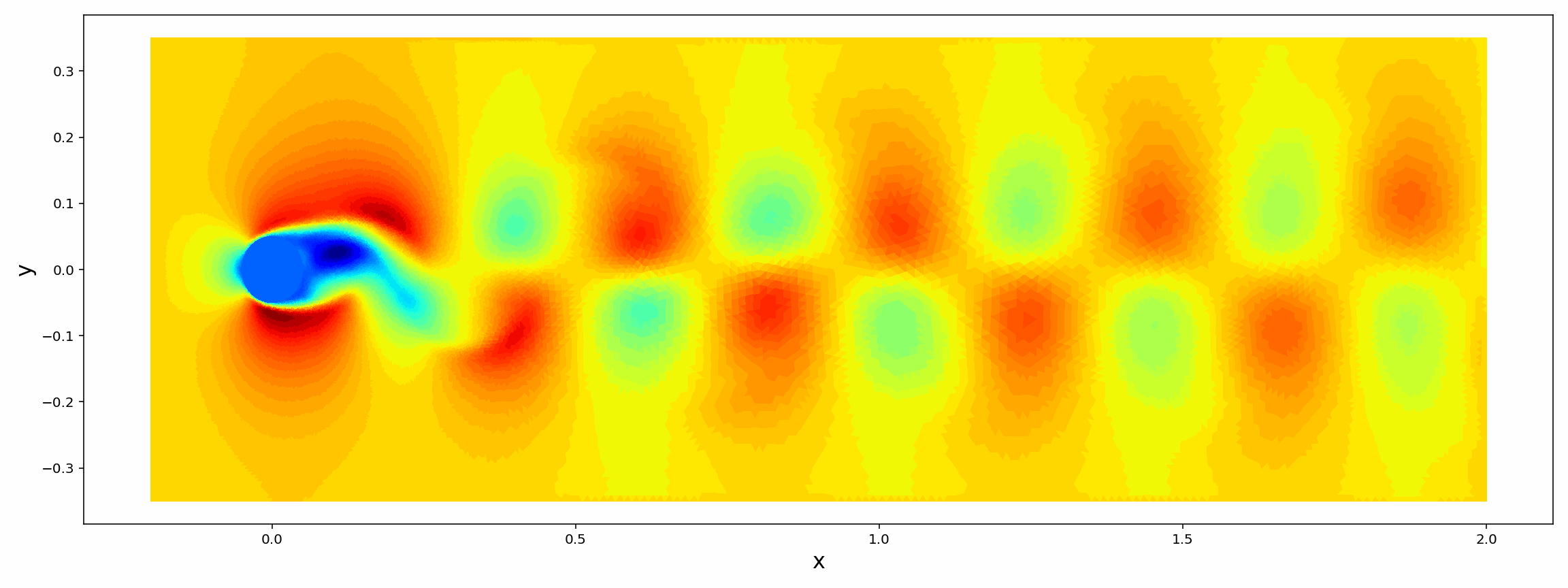
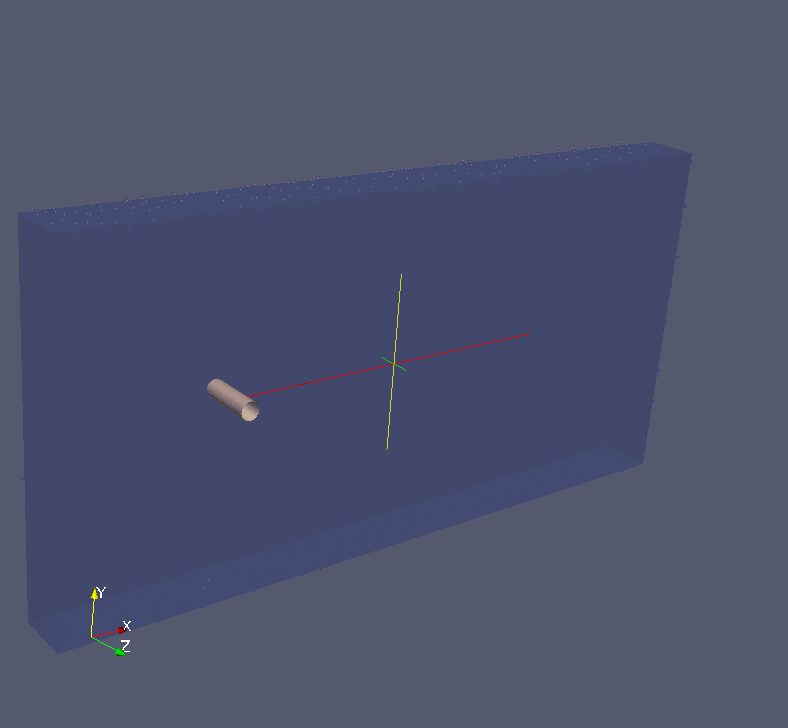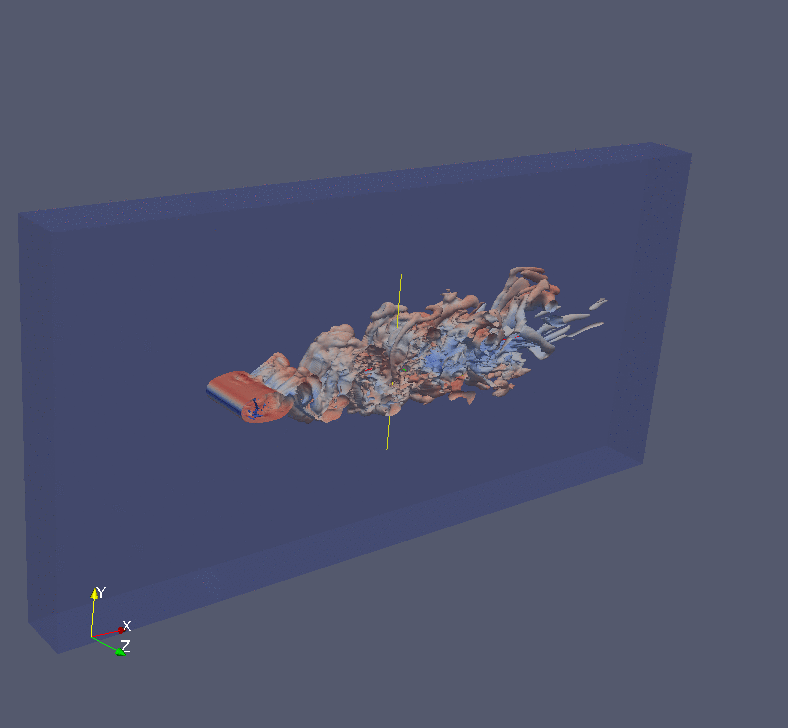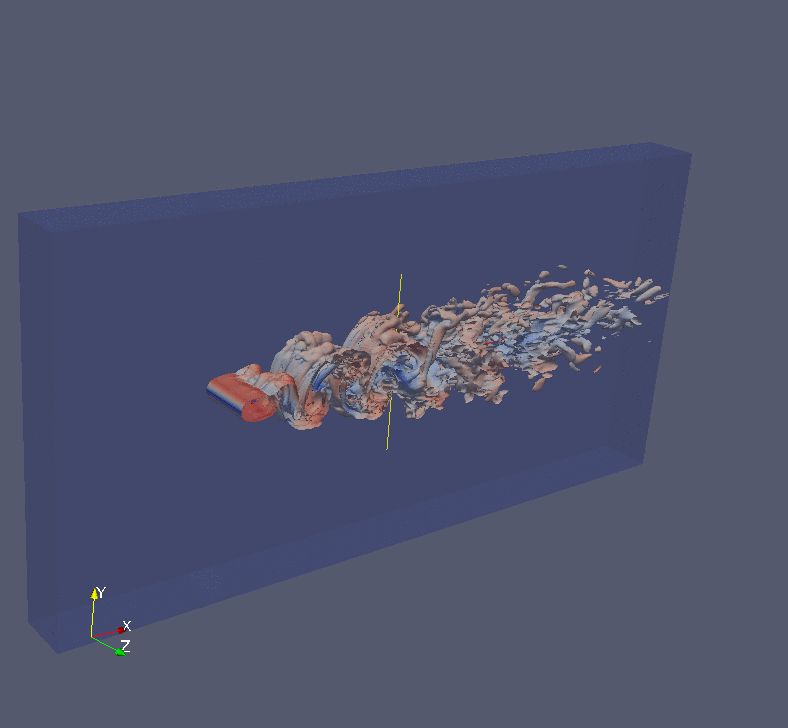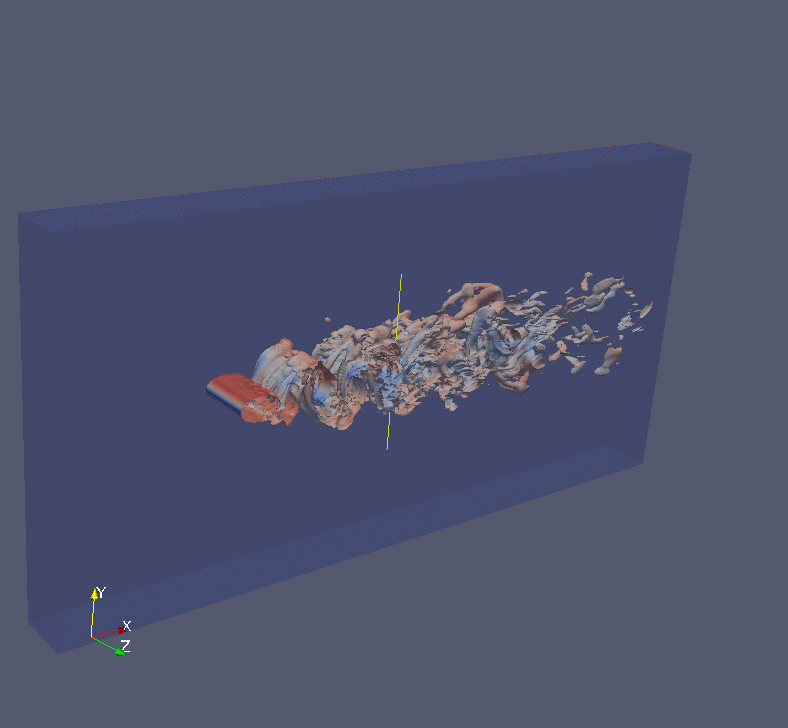
Analytic Continuation of Noisy Data in Quantum Many-body Physics Using Multistep ResNet

We propose a data-driven learning framework for the analytic continuation problem in numerical quantum many-body physics. Designing an accurate and efficient framework for the analytic continuation of imaginary time using computational data is a grand challenge that has hindered meaningful links with experimental data. The standard Maximum Entropy (MaxEnt)-based method is limited by the quality of the computational data and the availability of prior information. Also, the MaxEnt is not able to solve the inversion problem under high level of noise in the data. Here we introduce a novel learning model for the analytic continuation problem using a Adams-Bashforth residual neural network (AB-ResNet). Additionally, the advantage of this deep learning network is that it is model independent and, therefore, does not require prior information concerning the quantity of interest given by the spectral function. More importantly, the ResNet-based model achieves higher accuracy than MaxEnt for data with higher level of noise. Finally, numerical examples show that the developed AB-ResNet is able to recover the spectral function with accuracy comparable to MaxEnt where the noise level is relatively small.

Data-driven learning model for the analytic continuation problem in numerical quantum many-body physics. The figure shows spectral density function prediction from the multistep neural network with noise level 1% (left) and 0.1%(right).

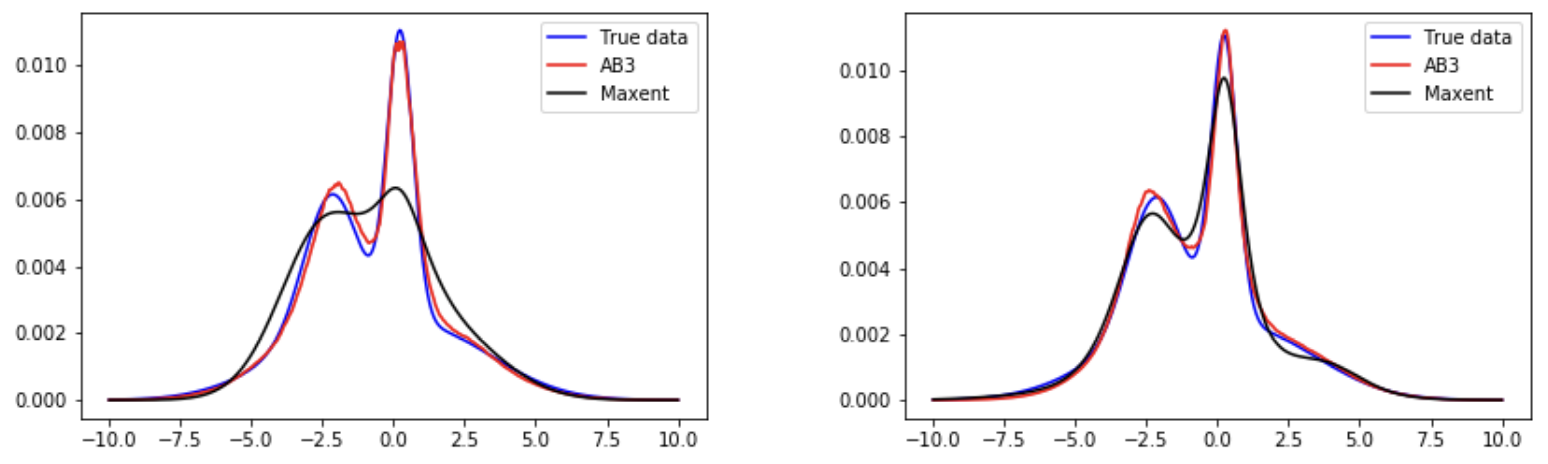
Paper:here

Presentations:DOE SciDAC-4 PI Meeting (2019), ORNL Computation Science Forum, ORNL Data Science Seminar

Latent Dynamics Learning for Stiff Collisional-radiative (CR) Models in Plasma Disruption Mitigation

Collisional-radiative (CR) models describe the atomic processes in a plasma by tracking the population density in the ground and excited states for each charge state of the atom or ion. These models predict important plasma properties such as charge state distributions and radiative emissivity and opacity. Accurate CR modeling is essential in radiative plasma modeling for magnetic fusion, especially when significant amount of impurities are introduced into the plasmas. In radiative plasma simulations, a CR model, which is a set of high-dimensional stiff ordinary differential equations (ODE), needs to be solved on each grid point in the configuration space, which can overwhelm the plasma simulation cost. In this work, we propose a deep learning method that discovers the latent space and learns its corresponding latent dynamics, which can capture the essential physics to make accurate predictions at much lower online computational cost. To facilitate coupling of the latent space CR dynamics with the plasma simulation model in physical variables, our latent space in the autoencoder must be a grey box, consisting of a physical latent space and a data-driven or blackbox latent space. It has been demonstrated that the proposed architecture can accurately predict both the full-order CR dynamics and the critical physical quantity of interest, the so-called radiative power loss rate.

Deep Reduced Physics model (deepRPM) architecture for CR models. The Grey box model contains the latent space discovery via physics integrated autoencoder and a dynamics learning neural network

DeepRPM architecture in the prediction stage. Full states prediction

Left figure shows the trajectories of the normalized charge state from the high-fidelity numerical simulation of the CR model for different initial conditions. The solution is for a single species, lithium, where the atomic number is 3. Four colored lines represent four charge states (they are partial sums of the solution state vector). Right figure plots the predicted trajectories under different temperature from our model.

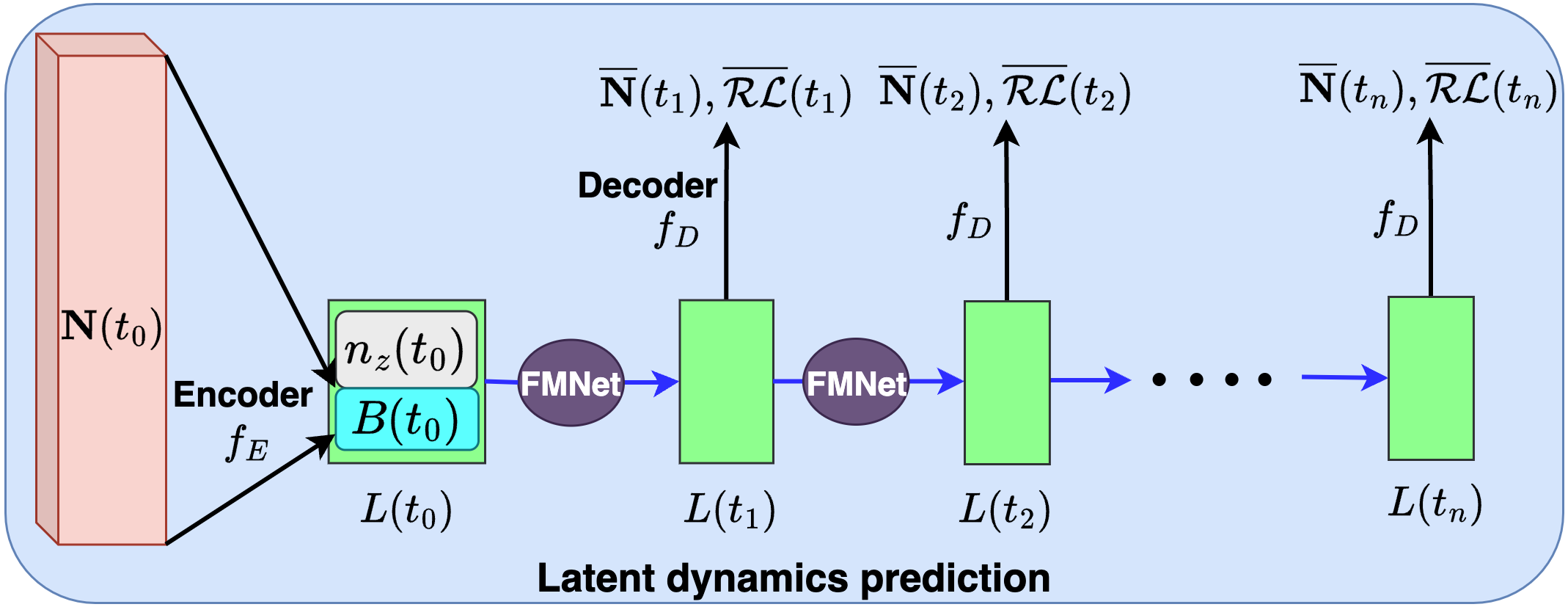
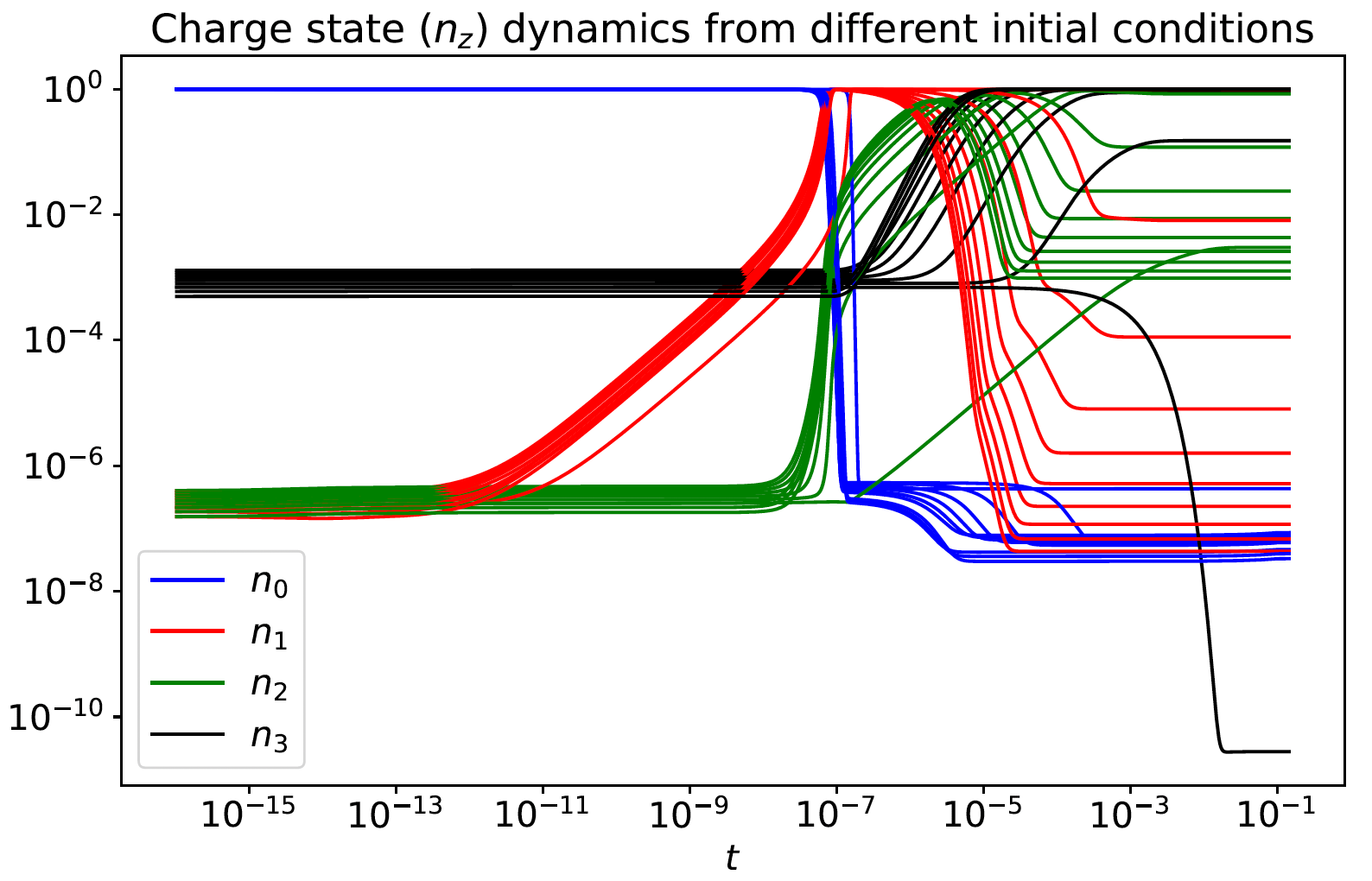
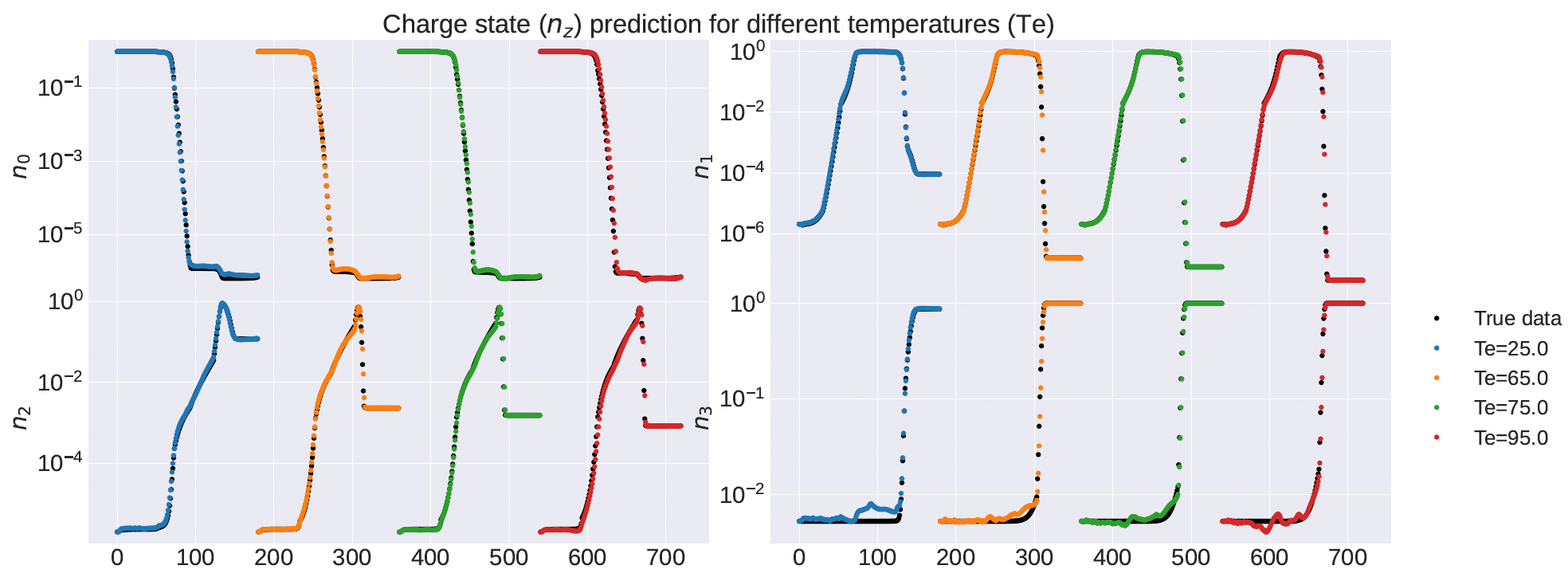
Paper: here, LA-UR-24-26289

Presentations: LANL T-5 ML Seminar (2023) DOE FES PI meeting on ML/AI (2024), AAAI Fall Symposium (2024)

Reduced Order Modeling (ROM)

In this area, I work on ROM for high-dimensional systems, focusing on applications in fluids, atmosphere, and ocean turbulence. A significant part of my research involves ROM closure and applications in data assimilation of turbulent flows.

Key topics include:

• ROM for turbulent flows
• Stabilization and ROM Closure modeling
• Applications to Atmosphere and Ocean turbulence (stratified rotating dynamics)

Data-driven Model Reduction of Atmospheric and Ocean Turbulence

Two dimensional Quasi-Geostrophic flow at \(Re=450, Ro=0.0036\). The vorticity field \(\omega\) is plotted from time \(t\in[30, 50]\)(left).

Two dimensional Rotating Turbulence modeling (Atmosphere) at \(30^o\) mid latitude Northern Hemisphere with Ekman damping. Strong rotation (bottom) vs weak rotation(top). Beta plane effect \(\beta\approx 1.6\times 10^{-11}m^{-1}s^{-1}\).

In the current study, we investigate rotational and stratified turbulent systems within the framework of the Boussinesq equations. The effects of rotation and stratification give rise to a variety of dynamical regimes in atmospheric and oceanic turbulence. To develop a better understanding of the fundamental flow properties through a more straightforward mathematical framework, we commence our research with a simplified two-dimensional Boussinesq model that incorporates rotation and stratification effects. We explore two distinct limiting dynamics, considering pure rotation and pure stratification separately. We examine these intriguing dynamics through numerical investigations, applying the exact solution theory of Boussinesq equations and examining small-scale perturbations to the exact solution under rotation and stratification. We conduct an analysis of statistical quantities associated with the turbulent state variables. The results indicate that, under weak rotation at the equilibrium statistical state, the flow field exhibits vortex flow. However, strong rotation transforms the flow into vertical shear flow. We observe both downscale and upscale energy transfers with a decay rate of \(k^{-3}\) in the absence of external forcing and dissipation. Furthermore, we delve into the study of internal gravity wave mode interactions in the simplified two-dimensional Boussinesq system, which is a crucial aspect of geophysical turbulence due to gravity. Our findings reveal that the time series of the mode coefficients exhibit wave-like interactions between wave modes. The mathematical model of atmosphere and ocean turbulence is the stratified rotating Boussinesq equation,

\begin{eqnarray} \frac{D^H\mathbf{u}_H}{Dt} + w\frac{\partial \mathbf{u}_H}{\partial z} + f\mathbf{u}_H^\perp &=& -\frac{1}{\rho_b}\nabla_H p &+ \mu\Delta\mathbf{u}_H +\mathbf{F}_H,\\ \frac{D^Hw}{Dt} + w\frac{\partial w}{\partial z} &=& -\frac{1}{\rho_b}\frac{\partial p}{\partial z}-\frac{g}{\rho_b}\rho &+ \mu\Delta w + \mathbf{F}_w, \\ \frac{D\rho}{Dt} + w\frac{\partial \overline{\rho}}{\partial z} &=& &\kappa\Delta\rho +\mathbf{F}_\rho,\\ \nabla\cdot \mathbf{u} &=& 0. \end{eqnarray} \begin{equation*} \mbox{With notation:} \frac{D^H}{Dt}=\frac{\partial}{\partial t} + \mathbf{u}_H\cdot\nabla_H, \,\,\,\,\,\,\, \nabla_H=(\frac{\partial}{\partial x}, \frac{\partial}{\partial y}),\,\,\,\,\, \nabla_H\cdot\mathbf{u}_H = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y},\,\,\,\,\, \mathbf{u}_H^\perp=(-v, u), \,\,\,\,\mathbf{u}=(\mathbf{u}_H, w) \end{equation*}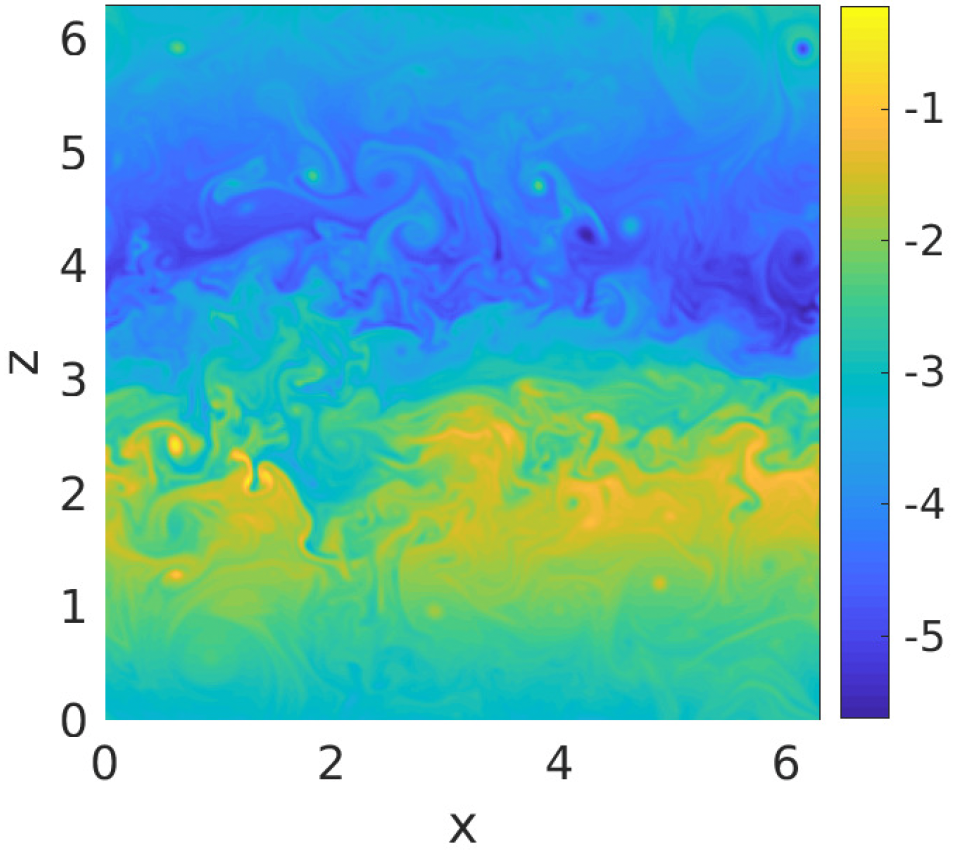

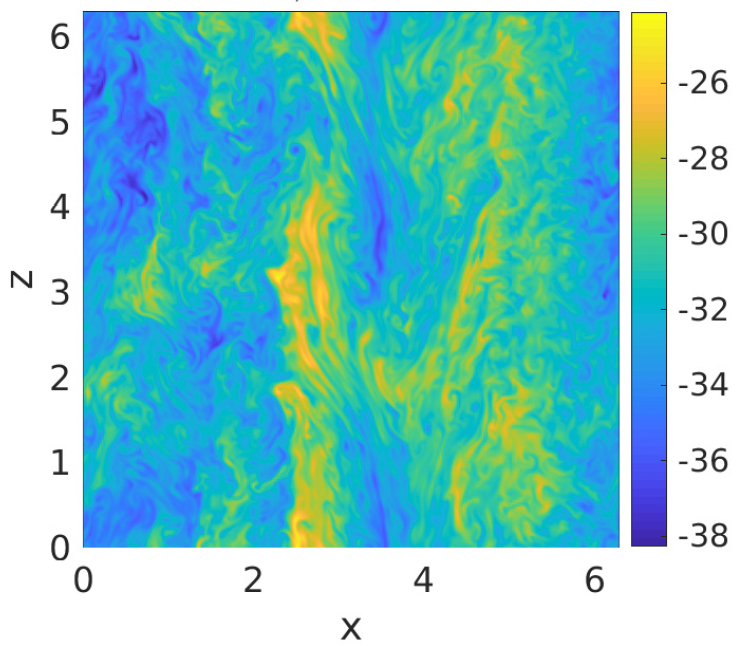
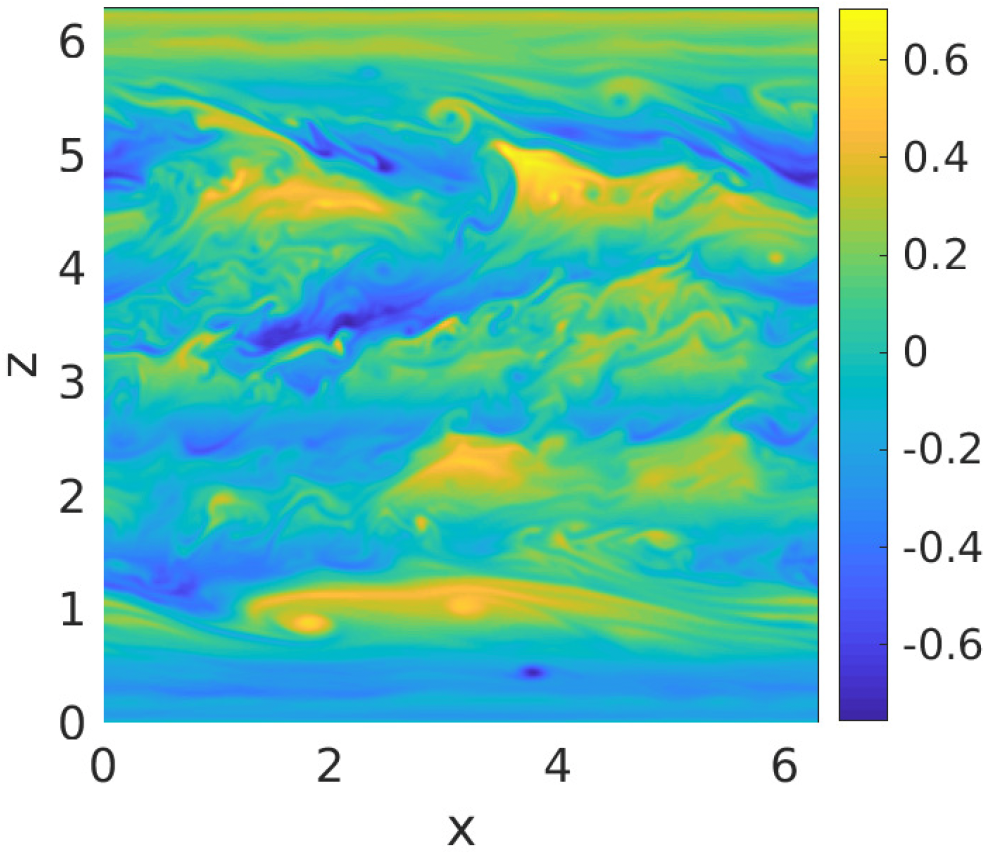
Boussinesq turbulence under strong stratification (left), strong rotation (right), and intermediate conditions (middle).

Paper: here

ROM Structural Closure: Approximate Deconvolution

The ROM closure model development was similar to the LES closure modeling development. Just as in LES, the first ROM closure models have been of the functional type. These functional ROM closure models have generally used some sort of stabilization procedure to model the effect of the discarded POD modes. Probably the first functional ROM closure model has been the mixing length model pioneered by Lumley and his group. This model was followed by more accurate ROM closure models, such as the Smagorinsky model, the variational multiscale model and the dynamic subgrid-scale model. As already mentioned, a physical motivation for the approach used to develop these functional ROM closure models is the concept of energy cascade. We emphasize that, just as in the LES case, these functional ROM closure models do not employ an explicit spatial filter; instead, they use phenomenological arguments to model the effect of the discarded POD modes. In this work, we use the approximate deconvolution (AD) method to put forth a new structural ROM closure model, the AD-ROM. Specifically, given the approximation of the filtered ROM variables, we use AD to obtain an approximation of the original unfiltered ROM variables and solve the ROM closure problem. Since the AD problem is notoriously ill-posed, we use a regularization method from image processing and inverse problems to obtain stable AD approximations.

3D flow past a cylinder with \(Re=1000\). Snapshots reconstruction from G-ROM (middle) and AD-ROM(right). Left figure is the DNS data.

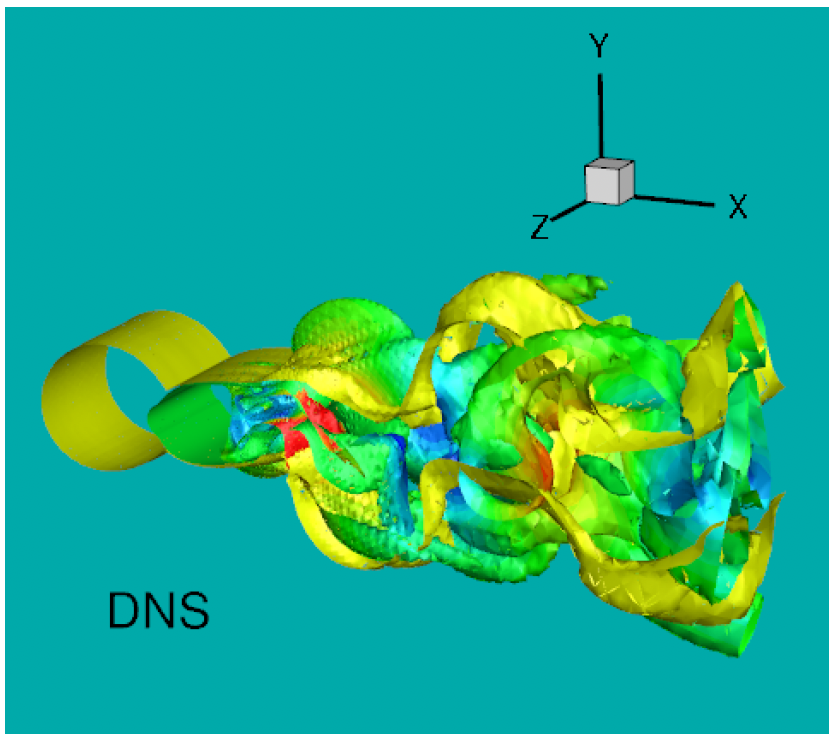
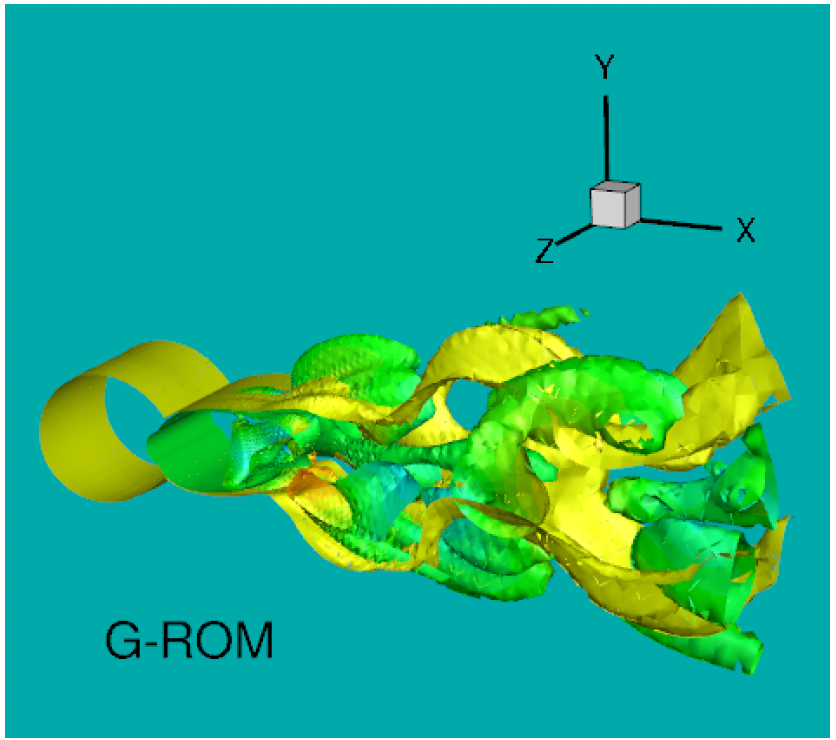
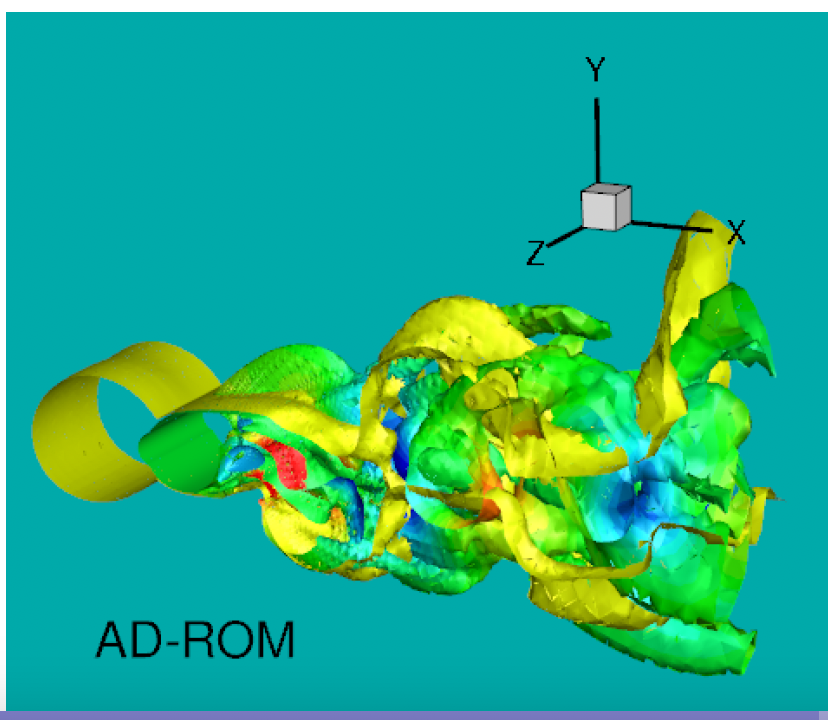
Paper: here

Presentations: Sandia National Laboratory (SNL) livermore Model Reduction Seminar (2017), ORNL Computation and Applied Math Seminar (2017), SIAM CSE (2017)

ROM Functional Closure: Data-driven Filter based on Large Eddy Simulation (LES)

In this work, we propose a data-driven filtered reduced order model (DDF-ROM) framework for the numerical simulation of fluid flows. The novel DDF-ROM framework consists of two steps: (i) In the first step, we use explicit ROM spatial filtering of the nonlinear PDE to construct a filtered ROM. This filtered ROM is low-dimensional, but is not closed (because of the nonlinearity in the given PDE). (ii) In the second step, we use data-driven modeling to close the filtered ROM, i.e., to model the interaction between the resolved and unresolved modes. To this end, we use a quadratic ansatz to model this interaction and close the filtered ROM. To find the new coefficients in the closed filtered ROM, we solve an optimization problem that minimizes the difference between the full order model data and our ansatz. We emphasize that the new DDF-ROM is built on general ideas of spatial filtering and optimization and is independent of (restrictive) phenomenological arguments

DDF-ROM provide stable energy conservation than G-ROM for 2D cylinder flow case.

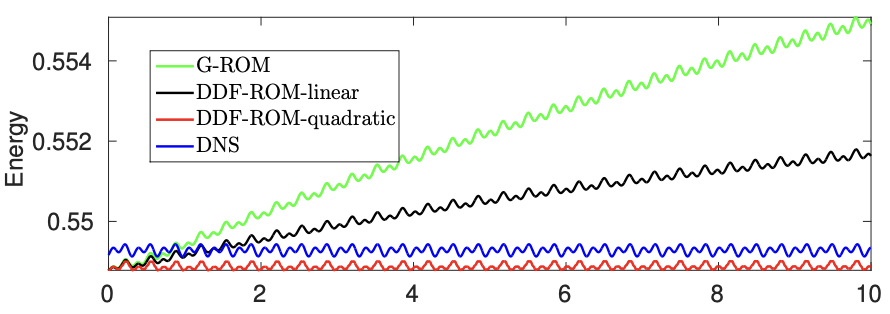
Paper: here

Presentations: SIAM CSE (2019), SIAM-SEAS (2019)